「推定」とは?
母集団から抽出された標本に基づいて、母数の値を推測することを推定という。
推定には1つの数値で母数を推定する点推定と、ある確率で母数が含まれる区間を推定する区間推定がある。
通常、標本平均はあくまで推定値であり、母平均とぴったり一致する訳ではない。
しかし、標本から「母平均はこの値からこの値までの範囲にある」ということはできる。
これを区間推定という。
区間推定は、母集団の従う分布が正規分布であると仮定できるときに、標本から得られた値を使ってある区間でもって母平均などの母数を推定する方法です。 このときの区間のことを「信頼区間」といいます。
どの範囲までを考慮するかというと、統計学では、伝統的に「95%の確率で母平均が含まれるような範囲」を使う。もっと厳しくしたいときには「99%の確率で母平均が含まれるような範囲」を使う。これをそれぞれ95%信頼区間、99%信頼区間と呼ぶ。
信頼区間の計算方法
実際に信頼区間を計算する。まず、母平均の推定値として、標本平均を使う。
次に、標本平均の分布の分散の推定値として、母分散をサンプルサイズで割ったものを使う。ここで、母分散は不偏分散で推定する。
標本平均の分散
標本平均の標準偏差
標本平均の標準偏差を標準誤差(SE:Standard Error)という。
信頼区間は以下の式で求める。
信頼区間=標本平均 ± t x 標準誤差
(ここで「t」は、信頼区間で決められた分布の面積が95% or 99%になるような数値。自由度(*サンプルサイズ-1)によって異なり、t分布表から読み取って使う。)
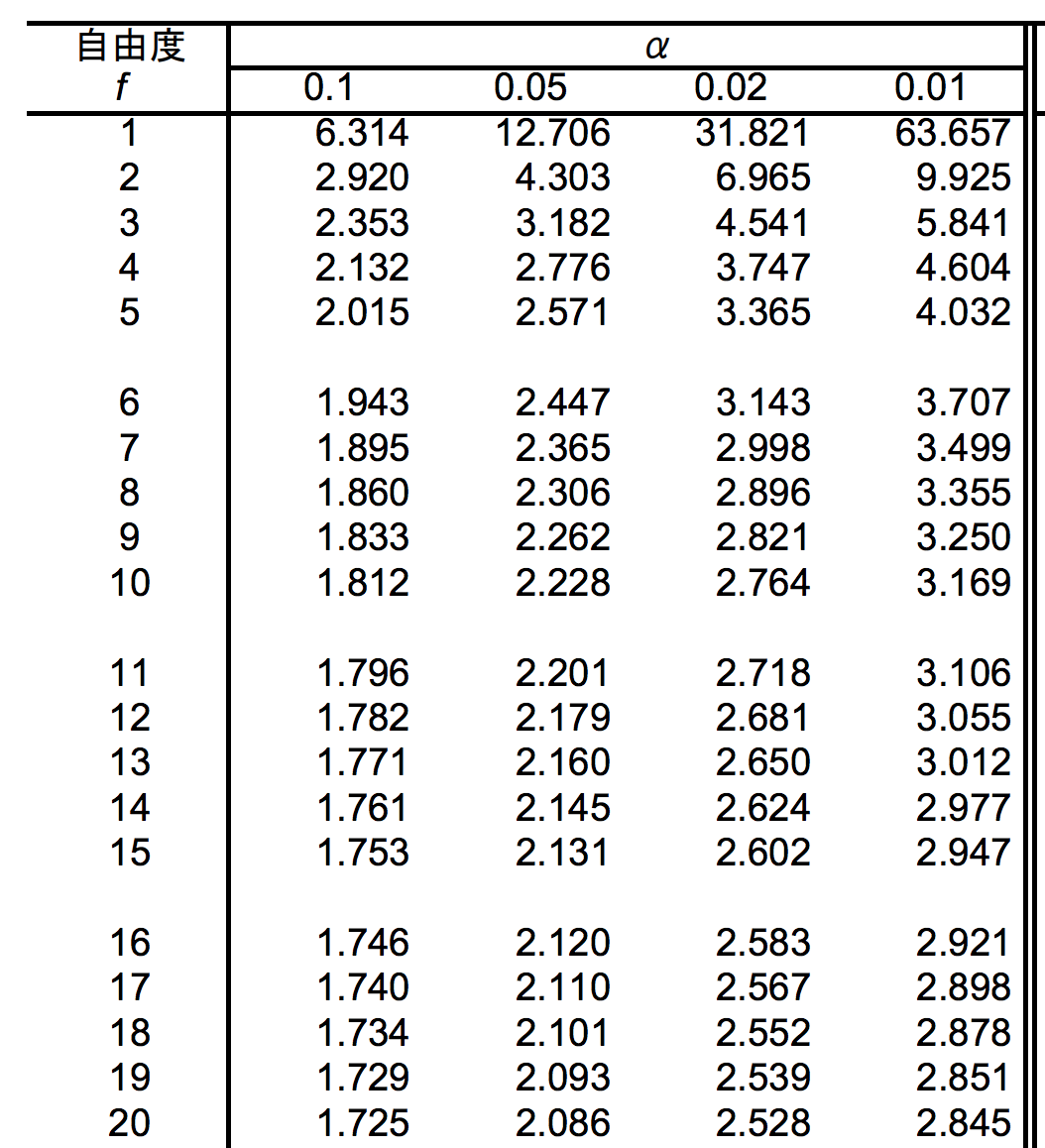
t分布表は統計学テキストの巻末には大体載っているし、ネット検索すれば出てくる。以下のような表だ。自由度と検証したい確率がクロスするところのt値を読み取る。正規分布の片側か両側かで確率が変わるが、それについては別途記事を書く。
t分布は自由度が小さい時は分布の山の形が正規分布よりも平べったくなり、自由度が大きいほど正規分布に近付く。要はサンプル数が多ければ多いほど正規分布に近くなり、少ないと裾野が広いグラフ形状で精度の悪い推定しかできないということだ。
http://www2.vmas.kitasato-u.ac.jp/lecture0/statistics/ttest.pdf
信頼区間を実際に計算してみて、母平均を推定できているか確認する
さて、ここまで来たところで標準誤差や母平均の信頼区間といったものを実際に計算してみる。
↑過去の記事で用いた平均10、標準偏差3の500個の正規分布に従うデータを使って確認をする。
関数で作った500個全データの平均が9.95であった。これを母集団の平均(=母平均)とする。この9.95は答えであるが、通常、母集団をすべて調査はできないので未知である。今回の例では、9.95と母平均を知っているのだが、一旦忘れてわからないとして、少ないサンプルから計算する標本平均を使って区間推定をする。
まずはt分布表からt値を出しておく。今回500個のデータの中からランダムに10個のデータを取り出すという設定なので、自由度は10-1=9である。
確率は95%としたいのでα=0.05をみて、これらがクロスする部分に記載されている数字がt値となる。(※片側2.5%ずつ、両側で5%)

t値=2.262とわかったので、後は標準誤差(SE)がわかれば信頼区間を推定できる。
計算したのが以下だ。

ランダムに取り出した10個のサンプルの平均(=標本平均)は「9.00」であった。
標準誤差は「0.93」であり、ここから95%の確率で母平均が含まれる範囲を推定すると
「6.89 ~ 11.11」の範囲にあると計算された。
今回の答え(母平均)は9.95であり、正しく推定できていることがわかった。
オレンジ色の文字はセルに入力した数式を示している。
