仮説検定とは？帰無仮説と対立仮説の設定にはルールがある

統計的推測：「仮説検定」とは？

母集団から抽出された標本に基づいて母集団の様子を推し測るのが統計的推測であり、その手法の内、母数に関する仮説が正しいかどうか判定することを仮説検定という。

仮説検定の設定は、検証しようとする仮説を帰無仮説 $H_0$ 、主張したい仮説を対立仮説 $H_1$ とする。

検定の結果、帰無仮説が正しくないとして、それを捨てることを統計的には棄却するといい、その場合は対立仮説が採択される。

棄却するかどうかの判断には統計検定量が使われ、その値がある範囲に入ったときに帰無仮説を棄却する。この棄却する範囲を棄却域という。

仮説検定の3つのステップ

仮説検定は大きく3つの手順に分けて考える。

１．仮説の設定

２．検定統計量と棄却域の設定

３．判定

◆１．仮説の設定

統計的推測ではまず仮説を立てるところからはじめる。

統計学の特徴的な考え方として、実際には差があるかどうかを検証したいのに、あえて「差はない」という帰無仮説を立てるということがある。

たとえば、あるイチゴ農園で収穫されるイチゴの重さが平均40g，標準偏差3gであったとして、イチゴの大きさをUPさせるため肥料を別メーカーのものに変えた。

成育したイチゴをいくつか採取（サンプリング）して、重さを測ったところ平均41.5g、標準偏差4gであった。肥料を変えたことによる効果はあったといえるか？

こういったことを統計的に効果の有無を判定すべく仮説検定は用いられる。

上記の例では、イチゴの肥料の変更による成育効果があったかどうかを検定したいが帰無仮説は「イチゴの肥料を変えたことによる収量の差はない」となる。

対立仮説は帰無仮説の反対なので、「イチゴの肥料を変えたことによる収量の差はある」となる。

◆「差はない」という帰無仮説を設定する理由

「差はある」という仮説は、「大きな差がある」「小さな差がある」「中くらいの差がある」など無限に立てられ、そのひとつひとつについて検討するのは事実上不可能である。

それに対して、帰無仮説の「差はない」というのは「変更前の特性＝変更後の特性」であり、イコールのこの形以外はない。なのでこれを採択するか、棄却するかを決めればよいことになり、単純化できるためにこのような仮説の設定が用いられる。

つまり、仮説検定とは、両者に違いがあるときに、それが誤差によって生じた違いか統計的に有意な違いかを判定する方法である。

仮説には、変化しているかどうかを検証する両側仮説、大きくなっているかどうかを検証する右片側仮説、小さくなっているかどうかを検証する左片側仮説があり、検証したい内容に応じて設定する。

２．検定統計量と棄却域の設定

帰無仮説と対立仮説を設定した後、次のステップは帰無仮説が正しいと仮定して、得られたデータが起こる確率（検定統計量）を計算する。

その確率が小さくて非常に稀にしか起こらない現象であるならば、帰無仮説を正しいとした仮定が誤っているとして、帰無仮説は正しくないと判断する。つまり、帰無仮説を棄却する。

稀かどうかの判断規準として有意水準αを設定する。これは危険率と呼ばれることもあり、通常5%あるいは1%が用いられる。

統計的検定では、理想的にはすべてのデータである母集団の特性を比較できれば良いが、現実的には困難なので、母集団から無作為に取得した少ない数のサンプルを用いて効果の有無を判断することになる。

なので統計的検定にはある程度の判断の誤りが付きものであり、以下のように表現する。

帰無仮説が正しいにもかかわらず、これを正しくないとして棄却する誤りを”第1種の誤り”、あるいは”あわてものの誤り”といい、αで表す。

逆に帰無仮説は間違っているのに間違っていると判断できない誤りを”第2種の誤り”、あるいは”ぼんやりものの誤り”といい、βで表す。

帰無仮説の誤りを正しく検出できる確率は1-βとなり、これを検出力という。

一般に有意水準を下げると検出力も下がるため、第1種の誤りを小さくすると第2種の誤りが大きくなる関係にある。表に整理すると以下のようになる。

f:id:yuinomi:20201017065613p:plain

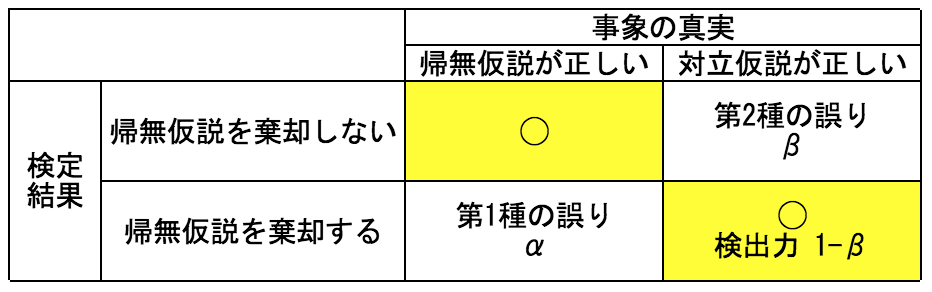
第1種の誤りをおかす確率は設定した有意水準αと同じである。有意水準5%としていた場合は、仮説検定による判定結果が20回に1回程度で間違った判断をすることが確率的には起こり得るということを意味する。

◆採択域と棄却域

有意水準αを5%としたときの採択域と棄却域の考え方を以下に示す。

f:id:yuinomi:20201016190057p:plain

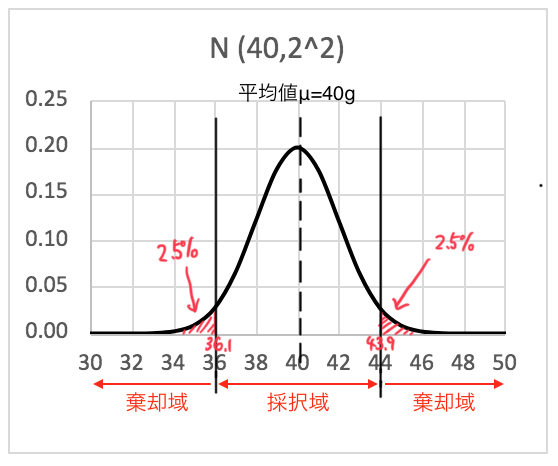
例は本記事で使ったイチゴ農園で収穫されたイチゴの重さ（平均40,標準偏差2）を使う。

有意水準が5%とは両側合わせて5%なので、下限側と上限側でそれぞれ2.5%ずつとなる。平均40,標準偏差2の正規分布で下限2.5%確率は36.08g、上限2.5%以上43.92gである。
つまり、実際に得られたデータの平均値が36.08~43.92gの範囲内であればデータのばらつきの範疇と見なし帰無仮説は棄却されない。しかし、それよりも小さかったり大きかったりした場合はめったに起きない低い確率が発生したことになり、母平均が元と同じではないと考える。