「交互作用」とは2因子の組み合わせによる効果
2つの因子を取り上げる実験では、2つの因子の”組み合わせ”による効果を考える必要がある。
組み合わせの効果を交互作用という。
因子Aと因子Bを同時に取り上げる時、交互作用がないというのは、一方の因子をどの水準に取っても他方の因子に影響がないということである。
一方、組み合わせ効果がある時には、Bの水準効果はAの水準によって変わる。
以下、具体的なグラフプロットでいろいろなパターンをみていく。
交互作用のない場合の例
例1)A、Bの主効果がともになく、交互作用もない

例2)Aの主効果はあるが、Bの主効果、交互作用はない

例3)A、Bの主効果がともにあるが、交互作用はない

交互作用のある場合の例
4)A、Bともに主効果があり、グラフが平行ではないので交互作用もある
(A2の水準効果がB1の方が大きい)

5)A、Bともに主効果があるが、B2ではAの水準効果はみられない

6)B1とB2でAの水準効果が逆になっている
A、Bともに主効果はないが、交差していることから交互作用がある

交互作用を実験で確かめるためには、すべての水準組み合わせで実験をする
2つの因子を取り上げる実験において、最適水準を見逃さないためには、必ずすべての水準組み合わせで実験をする必要がある。
例として、因子Aが3水準、因子Bが2水準の二元配置実験を行った結果が以下だったとする。グラフにプロットしたものを右側に示す。

この実験では因子A:3水準x因子B:2水準=6通りすべての水準組み合わせを実験している。特性値は数字が大きいほど良いとすれば、これらの組み合わせの中で最適水準はA3B2の35になる。
この実験を別の方法で行うことを考える。
まず、因子Aの中で最も良い水準を探すために因子BをB1に固定し、因子AだけをA1、A2、A3と振って実験する。
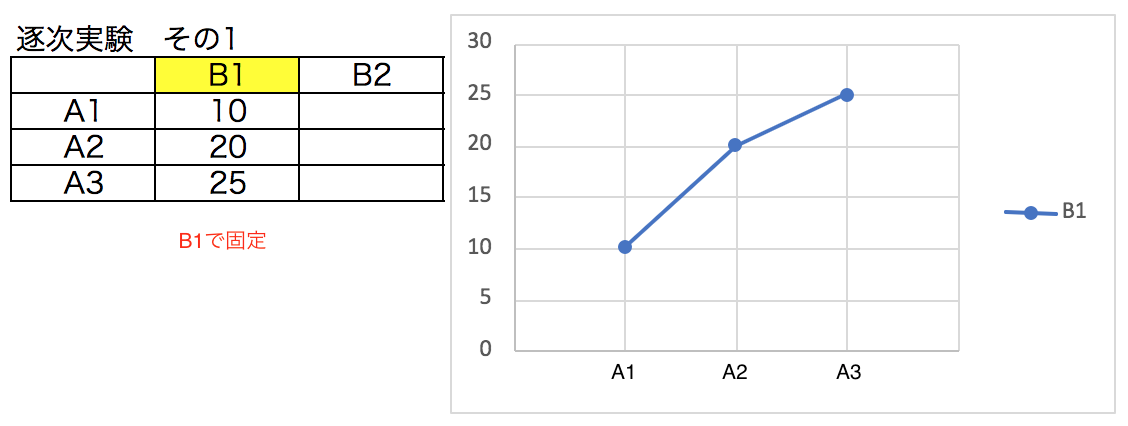
因子Aの中では、A3が最も良いことがわかった。
次に因子Bの中で最も良い水準を探すために因子AをA3に固定し、因子BだけをB1、B2と振って実験する。

B1とB2では、B2の方が特性が大きいことがわかった。
よって、2回の実験からA3とB2の組み合わせであるA3B2が特性値35で最適であることがわかった。

このような実験の仕方を「逐次実験」という。
すべての組み合わせで実験を行わずとも最適水準を探し出すことができた。
今回の3水準x2水準=6通りの組み合わせがある実験では、上図の表でグレイにした部分の実験を省略しているが、最適水準には問題なく到達できている。
逐次実験は、組み合わせの効果を考えず、因子Aと因子Bを独立したものとして取り扱う場合には有効である。
一方、組み合わせの効果(=交互作用)がある場合では、逐次実験では最適水準を見逃す可能性がある。二元配置実験ですべての組み合わせを実験すると、以下のような結果になる例があったとする。
交互作用があり、最適水準はA2B2の35である。

本来、すべての組み合わせで実験を行った時に上記の結果が得られていたものが、仮に逐次実験で行われたとする。
まず、因子Aの中で最も良い水準を探すために、因子BをB1に固定して、因子AをA1~A3で振って実験をした。その結果、A3が最も良いことがわかった。

次に因子Aは最も良かったA3に固定して、因子Bの中で最も良い水準を探す。
実験の結果、B1が最も良いとわかり、逐次実験の結果、最適水準はA3B1で特性値は25だった。

だが、これは間違いである。
すべての組み合わせで実験をしていれば、最適水準はA2B2で特性値35が探し出せたものが、交互作用があるのに逐次実験で計画したために、最適水準をA3B1の特性値25と誤判定してしまった。
通常、実際に実験を計画する場面で、その対象に交互作用があるかどうかを確実にわかっている時はむしろ稀で、どちらかわからない場合は、交互作用を見逃さないためにすべての水準組み合わせで実験を計画すると良い。
交互作用をみるためには、すべての水準組み合わせと”繰り返し”が重要
交互作用の有無の判断は、プロットしたグラフが平行かどうかを見れば良いとわかったが、通常データはばらつきを持つので、ぴったり平行とはならない。
少しのずれがある場合、交互作用により平行からずれたのか、誤差により平行からずれたのかをどのように判断するかを考える。

上図のようなデータがあったとする。交互作用がない場合、B1を基準としてA1、A2の水準効果がB2にもそのまま適用されるので、A2B2は黒点線で示したプロットになるはずだが、実験の結果オレンジのプロットとなった。
これが交互作用による効果か、単なる実験ばらつきによるものかを見極めるには、
すべての水準組み合わせの実験を”繰り返し”をして行う。
繰り返しを入れてその平均を取ることで、交互作用の有無をより明確に判断しやすくなる。
