【相関分析】無相関の検定

無相関の検定

母集団における相関係数、すなわち、母相関係数ρが0か否かの検定を無相関の検定という。仮説は以下のようになる。

　帰無仮説 $H_0$ ：ρ=0

　対立仮説 $H_1$ ：ρ≠0

一般的にデータ数が少ない時、統計量の信頼性は低い。得られたデータから求めた相関係数rに意味があるのか、誤差の範囲なのかを評価するために無相関の検定を行う。

この検定にはr表を用いる検定とt表を用いる検定がある。

r表による検定

r表を用いる場合、自由度はn-2となり、r表の数値はr(n-2,α)と表現する。

有意水準αにおける検定では、次のような規則となる。

|r| ≧ r(n-2,α)ならば $H_0$ を棄却する

|r| ＜ r(n-2,α)ならば $H_0$ を棄却しない

検定の概要としては以上だが、例題を使って実際に検定してみたい。

ある製造条件xと品質特性yの関係を考える。品質特性yは値が大きいほど望ましいとする。サンプルサイズはn=12で以下のデータを得た。

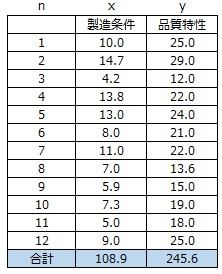
製造条件xと品質特性yに相関関係があるかを考えていく。はじめに散布図を作成して、グラフから視覚的にデータの関係性を確認する。

データプロットから正の相関がありそうということがわかる。

次に相関係数rを検討する。相関係数とは、相関関係の強さを示す尺度で次式により求められる。

$r = \dfrac{S_{xy}}{\sqrt{S_{xx} × S_{yy}}}$

xの偏差平方和 $S_{xx}$ 、yの偏差平方和 $S_{yy}$ 、xとyの偏差積和 $S_{xy}$ を求めるために、以下のような表を作成する。

与えられたデータxとyの二乗と積、合計をそれぞれ計算した。さらにここから以下の式で偏差平方和、偏差積和を求める。

$S_{xx} = \sum\limits_{i=1}^n (x_i - \bar{x})^2 = \sum\limits_{i=1}^n x_{i}^2 - \dfrac{\left(\sum\limits_{i=1}^n x_i \right)^2}{n}=1121.3 - \dfrac{108.9^2}{12} = 1121.3 - 988.3 = 133.0$

$S_{yy} = \sum\limits_{i=1}^n (y_i - \bar{y})^2 = \sum\limits_{i=1}^n y_{i}^2 - \dfrac{\left(\sum\limits_{i=1}^n y_i \right)^2}{n}=5315.0 - \dfrac{245.6^2}{12} = 5315.0 - 5026.6 = 288.3$

$S_{xy} = \sum\limits_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) = \sum\limits_{i=1}^n x_iy_i - \dfrac{\left(\sum\limits_{i=1}^n x_i \sum\limits_{i=1}^n y_i \right)}{n}=2389.7 - \dfrac{108.9×245.6}{12} = 2389.7 - 2228.8 = 160.9$