正規分布とは

正規分布とは、平均を中心にした左右対称の釣鐘形の分布で、その確率密度関数f(x)は以下の式で表される。別名、ガウス分布やベル・カーブとも言われる。
π:円周率 e:自然対数の底(2.718…) μ:平均値 :分散
正規分布は平均値μと分散によって分布の形状が定まり、一般にN(μ、
)と表す。
平均値μで横軸におけるグラフの最も高い位置(確率密度関数が最大)が決まり、分散の大きさでグラフのシャープさが決まる。分散が小さいほど急峻なカーブとなる。
以下に平均値μ=0で同じで、分散が、
、
の正規分布グラフの比較を示す。

正規分布の基本の使い方:μ±Xσで確率予測
正規分布は平均値μと標準偏差σを使って、データが取り得る確率を予測するのに使われる。
言葉だけでは少し分かりにくいので、具体的な例を挙げながら確認する。
注)分散はであり、
なので
例)マシュマロを大量に購入し、重さを測定した。測定してみると、平均値は10g・標準偏差は1gであった。
つまり、N(10,)の正規分布であり、グラフ化すると以下のようになった。

平均値である10gを中心に左右均等にデータの分布が確認できる。
さて、ここで例えばマシュマロの重さが9~11gのものは全体の中でいくつあるのかを調べたい時、平均値10gを中心に+,-方向に1gなので、「10±1g」となり「68.27%」となる。

正規分布な便利なところは、平均値と標準偏差が分かっていれば任意のデータ範囲が含まれる確率が平均値と標準偏差がいくつであるかに関わらず同じであることだ。
どのような正規分布の形状であっても、正規分布でさえあれば、確率計算が可能だ。
平均値μ±Xσで標準偏差X範囲内にデータが含まれる確率の代表的な例を示す。

先ほどのマシュマロの例では標準偏差1gなので、2.0σは2gになる。
10±2g(8~12gの範囲)に含まれるデータの確率は、上記表から95.45%となる。
逆にそれ以外の個体が検出される確率は表より4.55%であるが、この時、下の図のように両側であることに注意が必要だ。

グラフの裾野の両端、青線部の合計が4.55%であり、言い換えると8gより小さいマシュマロを引き当てる確率が2.28%、12gより大きい確率も同じく2.28%であるということだ。
この考えは正規分布の考えの基本なので、確実に理解しておく。
*ちなみになぜ急に例がマシュマロ?と疑問に感じられてた方もいるかもしれませんが、たまたま私がこの記事を書きながら「チョコまん」を食べていただけでそれ以上の深い意味はありません。
正規分布の標準化(=規準化)
正規分布N(μ、)に従う確率変数Xに数値変換
をすると、XをN(0,)に変換することができ、これを標準化(あるいは規準化)と言う。
このとき、置き換えたZも確率変数となり、確率変数Zは平均値(期待値)=0、分散=の正規分布に従い、このような正規分布N(0、
)を標準正規分布と言う。
μやσがどんな値であっても上記の式に置き換えればどんな正規分布でも必ず標準正規分布に置き換えることができる。
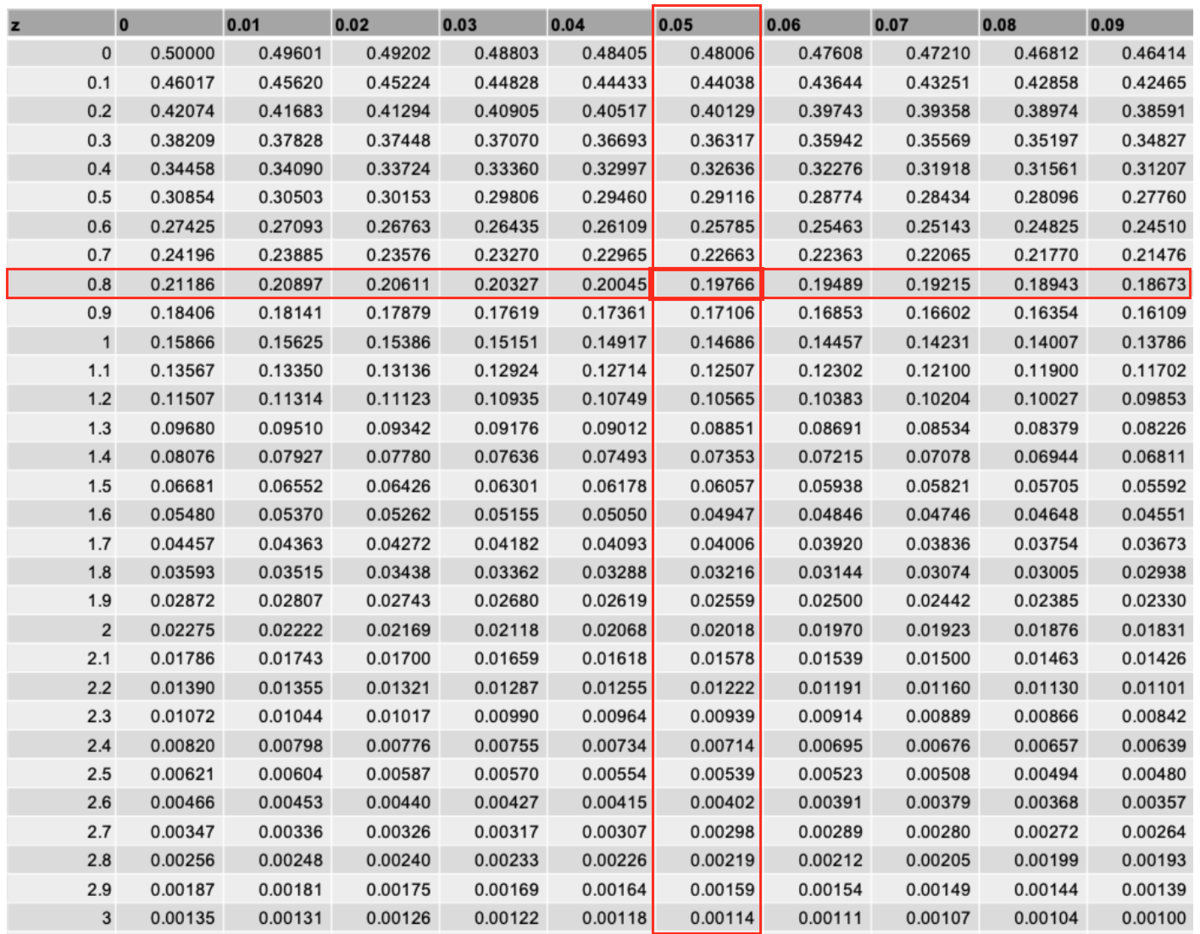
正規分布表を以下に示す。


出典:https://best-biostatistics.com/summary/standard-norm.html
表に数字がびっしりと並んでいるが、これはグラフに青斜線部で示した確率変数Zより右側の確率を意味している。
先ほどのマシュマロの例(平均値10、標準偏差1)で考える。
マシュマロをランダムに選び出し、例えばそれが10.85gより大きい確率は
となる。
正規分布表で縦軸:小数点以下1桁目が0.8、横軸:小数点以下2桁目0.05がクロスするところの数字を読み取ると「0.19766」となっているので、確率19.766%だとわかる。
このように、Zとは平均値μからの距離が標準偏差の何倍であるかを示し、右側確率とも言われる。
先ほどの計算で平均より0.85g大きい確率は19.766%だとわかったが、正規分布は左右対称のため、反対に平均より0.85g小さい確率(=9.15gより小さい確率)も19.766%である。
エクセルで正規分布を描く
正規分布のグラフをエクセルで描く方法は非常に簡単だ。
平均値μと標準偏差σだけ定義すれば、NORM.DIST関数を使ってさっと確率密度関数を計算できる。
![]()
一例として、平均5,標準偏差1の正規分布を描く。
C6セルに下図赤字のように入力してドラッグすれば完了だ。この時、平均と標準偏差はドラッグした時に動いてほしくないので、$マークを付けて絶対参照にしている。
関数形式は確率密度関数を描きたい場合は「FALSE」or「0」、累積分布関数を描きたい場合は「TRUE」or「1」を選択する。

平均5,標準偏差1の確率密度関数と累積分布関数をそれぞれ以下に示す。

数値表を使わず、確率分布をエクセルで一発計算する方法
正規分布を標準化して数値表から確率を読み取れるのはわかったが、毎回数値表を参照するのも手間なので、最後にエクセル関数を使って一発で計算する方法を示す。
実際の仕事にも即適用できるので是非覚えておきたい。
確率変数XがZ以下の値を確率をPとする時、Zから確率Pを求めるのがNORM.DIST関数で、反対に確率PからZを求めるのがNORM.INV関数である。
正規分布を標準化(規準化)している場合は、
NORM.S.DIST(Z,関数形式)・・・確率を計算
NORM.S.INV(Z,関数形式)・・・%点を計算
で計算可能だが、より仕事を効率化するために標準化をしないでいくつか具体例を挙げて順番に確認する。
標準化をしていない場合は、
NORM.DIST(x,平均,標準偏差,関数形式)・・・確率を計算
NORM.INV(x,平均,標準偏差,関数形式)・・・%点を計算
とエクセルに入力する。
関数形式は、確率密度関数を求めたい場合は「0」or「FALSE」、累積分布関数を求めたい場合は「1」or「TRUE」と入力する。
【例1】平均10,標準偏差1の正規分布で11以下の確率
NORM.DIST(11,10,1,TRUE)=0.8413=84.13%

【例2】平均10,標準偏差1の正規分布で11以上の確率
1-NORM.DIST(11,10,1,TRUE)=1-0.8413=0.1587=15.87%

【例3】平均10,標準偏差1の正規分布で8以下もしくは12以上となる確率
NORM.DIST(8,10,1,TRUE) + 1-NORM.DIST(12,10,1,TRUE) =0.0275 + 0.0275=0.0455=4.55%

【例4】 平均10,標準偏差0.8の正規分布で左側5%確率となるデータ
NORM.INV(0.05,10,0.8)=8.68 よって、データが8.68以下となる確率が5%

【例5】 平均10,標準偏差0.8の正規分布で右側5%確率となるデータ
NORM.INV(0.95,10,0.8)=11.32 よって、データが11.32以上となる確率が5%

【例6】平均10,標準偏差0.8の正規分布で両側5%確率となるデータ
両側の場合は左側2.5%、右側2.5%と分割して計算する
NORM.INV(0.025,10,0.8)=8.43
NORM.INV(0.975,10,0.8)=11.57
よって、8.43以下あるいは11.57以上となる確率が5%
(逆に言えばデータが8.43~11.57の範囲内である確率は95%)

上記6つのパターンの使い分けさえできれば正規分布の計算は実務上ほぼ困ることはないはずだ。
![図解入門 よくわかる最新実験計画法の基本と仕組み[第2版] 図解入門 よくわかる最新実験計画法の基本と仕組み[第2版]](https://m.media-amazon.com/images/I/514nRQSv1sL._SL160_.jpg)
