↑前回の記事の続き。
データは『統計学がわかる』p15,第1章「ポテトの長さは揃ってる?」を参考にしている。
ワクワクバーガーとモグモグバーガーの2つのお店で49本ずつのポテトの長さを度数分布(ヒストグラム)を作って比較した。

データをグラフ化することで、視覚的にそれぞれのお店の特徴がわかりやすくなり、モグモグバーガーの方がデータのばらつきが大きいことがわかった。
今回は、このばらつきを数字で表してみる。
分散の計算
分散とは、データの散らばりの度合いを表す値です。 分散を求めるには、偏差(それぞれの数値と平均値の差)を二乗し、平均を取ります。 なお、分散の正の平方根が標準偏差となります。 -Sci-prusuit
分散=((データ - 平均値)2)の総和÷データ数 で求めることができる。
簡単な例題で計算してみる。以下のような5つのデータがあったとしよう。

平均はAVERAGE関数で計算し、5となる。
次に各データと平均との差を求め、さらにそれらを2乗する。

オレンジ色の文字でセルに入力した関数を示した。
「平均との差の2乗」の総和 が I10セルで計算されており、今回の例では10となった。これをデータ数の5で割ると分散2が求められる。
分散は、平均値を中心にして、データがどのくらいばらついているかを意味する数値だ。
単位は今回の例の場合、個々の実験データがcmであり、分散は計算の過程で2乗しているため
cm2(平方センチメートル)となる。単位が異なることに注意。
ちなみに平均との差を2乗するのは、正負の影響を排除するためであり、データ数で割るのは、この作業をしないとデータサンプル数が多ければ多いほど分散が大きくなってしまうのを防ぐためだ。
よって、今回のエクセルシートでは平均との差を「各データ - 平均」で計算したが、これを逆にしても個別の平均との差は変わるが、2乗して総和を出すので分散の結果は変わらない。平均との差を入れ替えたパターンを以下に示す。
(「A-B」を「B-A」にした。)

平均との差のセルは、先の計算と符号反転しているが、2乗しているので分散の結果は同じとなる。
標準偏差の計算
次に標準偏差を求める。
標準偏差 (、英: standard deviation、SD)は、分散の正の平方根である。データや確率変数の散らばり具合(ばらつき)を表す指標の一つである。例えば、ある試験でクラス全員が同じ点数、すなわち全員が平均値の場合、データにはばらつきがないので、標準偏差は 0になる。
標準偏差の計算は簡単で、以下の式で計算できる。
標準偏差=√分散
今回の例では分散が2なので、標準偏差は
√2=1.414となる。
これで分散と標準偏差の計算ができた。
エクセルの関数を使ってさっと計算する
次にさきほど手順通り計算した分散と標準偏差を、エクセルの関数機能を使って最短で計算する。

先ほどの計算では、分散を求めるにあたって、データの平均値や、データと平均との差を計算したりしたが、エクセルの関数機能を使ってデータからダイレクトに分散と標準偏差を計算することもできる。
セルに入力した関数をオレンジ色の文字で示した。
分散の計算にはVAR.Pを、標準偏差の計算にはSTDEV.Pを使う。
注)VAR.P関数は「標本分散」の計算に使う。「不偏分散」を求めたい時はVAR.S関数となる。
さて、ここまで来たところで練習問題に戻って、ワクワクバーガーとモグモグバーガーのポテトの長さについて分散と標準偏差を比較する。
2つのお店のポテトの長さは以下のようなデータであった。
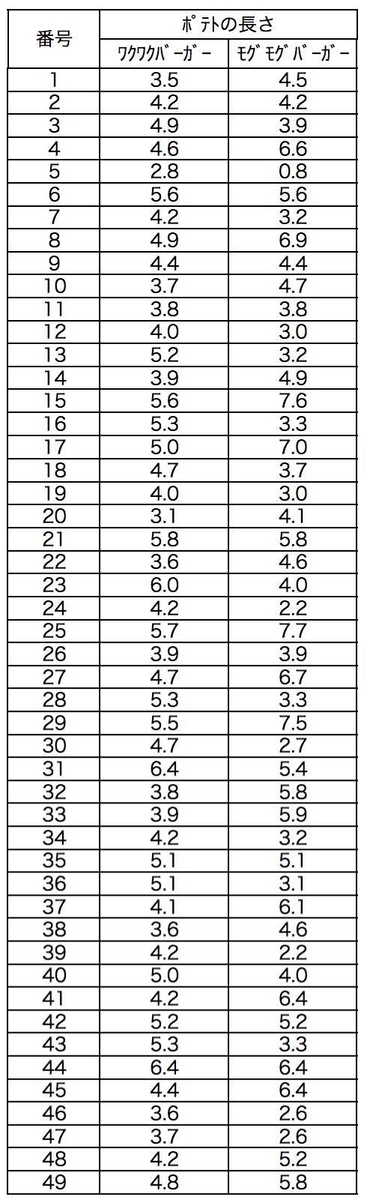
便利なエクセル関数 分散VAR.Pと標準偏差STDEV.Pを使って一発で計算すると

このようになり、ヒストグラムでなんとなく把握できていたデータの特徴(ワクワクバーガーはデータが平均値を中心に安定しているが、モグモグバーガーは全体にムラがありばらつきが大きい)が、分散と標準偏差によって数値化して再確認できた。
ちなみに分散と標準偏差を上の例では、エクセル関数を使って瞬時に求めたが、平均との差を使って順序通りに計算しても過程(手間)は増えるだけで当然同じ結果を出すことができる。
試しにワクワクバーガーで49個のデータから分散と標準偏差を計算すると以下のようになった。

データ番号の11~47は表示の都合上、省略しているが、49個のデータを使って「平均との差」「平均との差の2乗」から分散と標準偏差を求めたが、エクセルの関数機能を使って一発で算出した結果と同じであることが確認できる。
