回帰分析(単回帰分析)の相関係数について、エクセルを用いて検討する。
JUSE‐StatWorksによる回帰分析入門 (StatWorksによる新品質管理入門シリーズ)
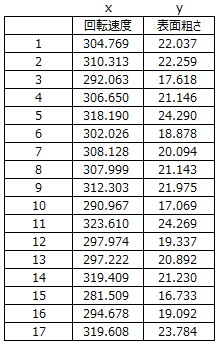
例1.1:旋盤の回転速度と表面粗さの関係_p1
旋盤で加工したある機械部品の表面粗さ(単位μ)と、それを加工した時の旋盤の回転速度の記録である。表面粗さの規格値は16~24μである。
表面粗さは、なるべくばらつきが小さくなるように管理したい。
もし旋盤の回転速度と表面粗さに何らかの関係があるならば、回転速度を管理することで表面粗さのばらつきを抑えたい。
散布図プロットで視覚的に判断する
xとyに相関があるかを確認するため、まずは散布図を描いてみる。
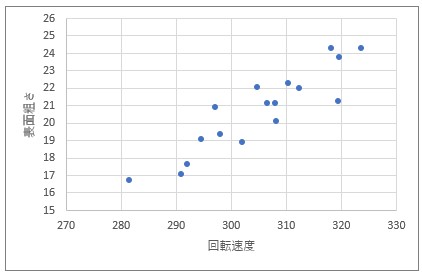
回転速度xを横軸、表面粗さyを縦軸として散布図をプロットした。
グラフから正の相関がありそうということが直感的にわかる。
xが増加するとyが増加する場合は、xとyに正の相関関係があるという。
逆にxが増加するとyが減少する場合は、xとyに負の相関関係があるという。
関係がない場合は、無相関であるという。
相関係数rの検討
次に相関係数rを検討する。相関係数とは、相関関係の強さを示す尺度で次式により求められる。
rは-1≦r≦1の範囲にあり、+1に近い場合は正の相関、-1に近い場合は負の相関があるという。また、0に近い場合は無相関であるという。
2つの変数xとyがあるときに、xの偏差平方和、yの偏差平方和
、xとyの偏差積和
はそれぞれ次式により求められる。nはサンプルサイズ(データ数)
エクセルで計算してみる。与えられたデータxとyの二乗と積、合計をそれぞれ計算する。
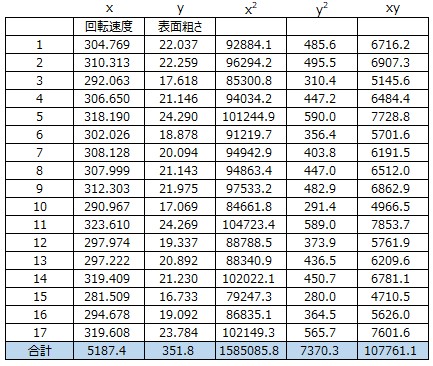
さて、これで偏差平方和と偏差積和をそれぞれ求めれたので、相関係数rを計算する。
相関係数rの値から相関係数の強さを判断するための目安は次の通り。
|r|が0.7以上 → 強い相関がある
|r|が0.4~0.7 → 中程度の相関がある
|r|が0.2~0.4 → 弱い相関がある
|r|が0.2以下 → ほとんど相関がない
今回の例題では相関係数rが0.906なので強い正の相関があることがわかる。
今回はステップを踏んで偏差平和和と偏差積和から計算して相関係数を求めたが、エクセルの便利な関数CORRELを使えば、自動計算で瞬時に相関係数rを計算できる。
=CORREL(配列1,配列2)
配列1にはxのデータ、配列2にはyのデータを指定する。
関数CORRELを使って計算すると[0.906374813]となり、上記の計算結果と一致する。
今回の例題では、与えられたデータ群をまず散布図グラフにプロットし、正の相関関係があることを視覚的に把握した上で、相関係数rを計算しその影響程度を数値的に解析した。
どちらかだけで判断するのではなく、両方の見方で評価することが重要である。
特に相関係数rだけでは、データの中の外れ値や集団を見落としたり、曲線関係にある場合などで相関係数rが小さく出てしまうことで2変量間に何かしらの関係があるにも関わらず、ないと誤判定してしまうリスクがあるので注意が必要だ。
寄与率 について
について
寄与率は、相関係数rの2乗で計算され、回帰式が予測の役に立つ式であるかを見るための統計量として用いられる。
エクセルで散布図を描いて、近似曲線(線形近似)を追加し、グラフのオプションから「グラフにR-2乗値を表示する」を選択することで表示できる。
試しに本ページ冒頭で作成した散布図プロットに近似曲線を追加し、数式とR-2乗値を表示してみる。

y=0.1821x-34.878 が回帰式を示し、=0.8215が寄与率である。
エクセルで乗値をこのように表示させると、結果だけが分かり、その計算プロセスは良く分からなかった。しかし今回、偏差平方和と偏差積和から相関係数rを計算し、
r=0.906 であることを確認しているので、
寄与率は
となり計算結果が一致することを確認できる。
