↑勉強中のテキスト。第6章「3つ目のライバル店現る - 分散分析(1要因)」
ワクワク、モグモグ、パクパクの3つのお店を比較する。
2つの標本間の平均の差を調べるのにはt検定が使えたが、標本が3つ以上になるとt検定を使うことはできないので、分散分析を使う。
テキストの例では、ワクワク、モグモグ、パクパクの3つのお店でポテトの味に差があるかを分散分析で調査している。まずはデータの入手で、それぞれのお店のポテト20個をランダムで試食してもらい、100点満点で採点した。採点した結果を以下に示す。

標本(サンプル)数はいずれの店も20個だ。
標本平均は高い順でパクパク88.15、ワクワク84.00、モグモグ79.50となった。
標準偏差についてはどの店も同程度のばらつきだ。
これを検定する場合、帰無仮説は「3つのお店のポテトの評価(母集団)の平均に差はない」となる。もう少し詳細にいうと「3つのお店のポテトの評価(母集団)の平均のどの組み合わせにおいても差はない」ということになる。
よって、対立仮説は「3つのお店のポテトの評価(母集団)の平均の少なくとも1つの組み合わせに差がある」となる。
注意)ここで、対立仮説は「すべての組み合わせに差がある」とはなっていないことに気を付ける
群間のずれと郡内のずれを理解する
全体平均からのズレ=群間のずれ+郡内のずれ で表される。
この群間のずれと郡内のずれとはそれぞれ何を意味するか、を理解することが重要だ。それぞれ簡単な図解で説明する。
◆郡内のずれ、とは?

上に母集団Aの正規分布を示した。母集団Aの平均(=母平均)は山の頂上の位置にある。この母集団Aから1つ標本を抜き取って測定したところ、測定結果はA1であったとする。
このとき、母平均からA1までの差が郡内のずれである。図では青色の矢印で示した。
下の図のようなパターンでもまったく同じである。山の頂上の右側にあっても同じ考えで、母平均と標本A2の差が郡内のずれで表現される。

郡内のずれは、その群(母集団)との個別の標本との差なので、すべての標本が異なる値を持つことになる。
◆群間のずれ、とは?
下の図のように母集団Aと母集団Bの2つがあったとする。(3つ以上であっても構わない)母集団Aと母集団Bのそれぞれの母平均を黒色の線で示した。さらにすべてのデータの平均というものもあり、それを全体の平均として緑色の線で示した。(「すべてのデータの平均」でも「母平均Aと母平均Bとの平均」どちらでも構わない。表現の仕方が異なるだけで計算結果は同じだ。)
緑色の線で示した「全体の平均」と「母集団Aの平均」の差が群間のずれである。

群間のずれは母集団の数だけあることになる。
さて、ここまで来たところで、もう一度全体の平均からのずれの考えを復習する。以下の式で表された。
全体平均からのズレ=群間のずれ+郡内のずれ

上の図のように母集団Aと母集団Bがあるとして、その中1つの標本A1を抜き取った時、それは全体の平均と母平均Aとのずれ(=群間のずれ)と、母集団Aの中でのずれ(=郡内のずれ)の両方を併せ持つということだ。
まとめると、分散分析の考え方とは、以下のようになる。
郡内のずれに比べて、群間のずれが大きければ、母集団同士の違いが大きいということになり、「母集団の平均に差がない」という帰無仮説を棄却することになる。
郡内のずれに比べて、群間のずれが小さければ、母集団同士の違いが大きいとはいえないため、「母集団の平均に差がない」という帰無仮説を採択することになる。
実際に分散分析の計算をしてみる
では、ここから実際に分散分析の計算をしてみる。前段の説明が長くなったので、今回の例題を再掲する。ワクワク、モグモグ、パクパクの3つのお店でポテトの味の評価に差があるか、を調べるという問題だった。各店のサンプル数は20だった。

では、順次計算をしていく。「分散分析」という名の通り、分散を分析する必要があるので、まずは標本分散を便利なエクセル関数VAR.P計算する。

例としてワクワク店のサンプルサイズ、標本分散の計算でセルに入力した数式をオレンジ色で右のG列に示した。偏差平方和(郡内の平方和)とは、平均と標本との差を2乗したものの総和を意味する。
偏差平方和=標本分散 x サンプルサイズ で計算しているが、
これをステップはやや複雑になるが、以下のように各店の標本平均との個別の標本との差の2乗を足し合わせても結果は同じになる。(背景が黄色セル20個の合計が580.00)

さて、ここまでの計算で、郡内の平方和=ワクワク580.00+モグモグ595.00+パクパク570.55=1745.55 がわかった。
次に、群間の平方和を求める。群間の平方和は以下の式で計算する。
群間の平方和=(郡内平均ー全体平均)2 xサンプルサイズ

計算結果を示す。全体の平均はワクワク、モグモグ、パクパクの60個データの平均値だ。
ワクワクの群間の平方和=(郡内平均84.00-全体平均83.88)2 xサンプルサイズ20=0.27となる。他のお店についても同様に計算する。これで、3つのお店についての郡内・群間の平方和が明らかになった。
これをまとめると以下のような表になる。

3つのお店についての郡内の平方和+群間の平方和が全体の平方和2494.18となる。
分散分析表をつくる
ここまでに計算した数値を分散分析表に入れて埋めていく。まずは偏差平方和を入力した。

次は自由度についてだが、
群間の自由度=群の数-1=3-1=2
郡内の自由度=(群1のサンプルサイズ-1)+(群2のサンプルサイズ-1)+(群3のサンプルサイズ-1)=(20-1)+(20-1)+(20-1)=57
全体の自由度=群間の自由度+郡内の自由度=2+57=59 となるので、それぞれを入力すると以下のようになる。
補足:全体の自由度は全データ数-1でも計算できる。

平均平方は平方和÷自由度で計算する。

今回の例では、
群間の平均平方=748.63÷2=374.32
郡内の平均平方=1745.55÷57=30.62 となる。
Fは群間の平方和÷郡内の平方で求める。374.32÷30.62=12.22だ。

ここまでやって、ようやく分散分析表が完成した。分散分析は、群間・郡内の平方和さえ最初に計算すれば、後の分散分析表を埋めていくこと自体は単純な計算のみで簡単だ。さて、あとはこの算出したF値12.22で、有意な差があるといえるかをF分布表と見比べて検定する。
F分布表は統計学テキストの巻末か手元になければネット検索ですぐに出てくる。エクセル関数で計算することも可能だ。
http://ktsc.cafe.coocan.jp/distributiontable.pdf
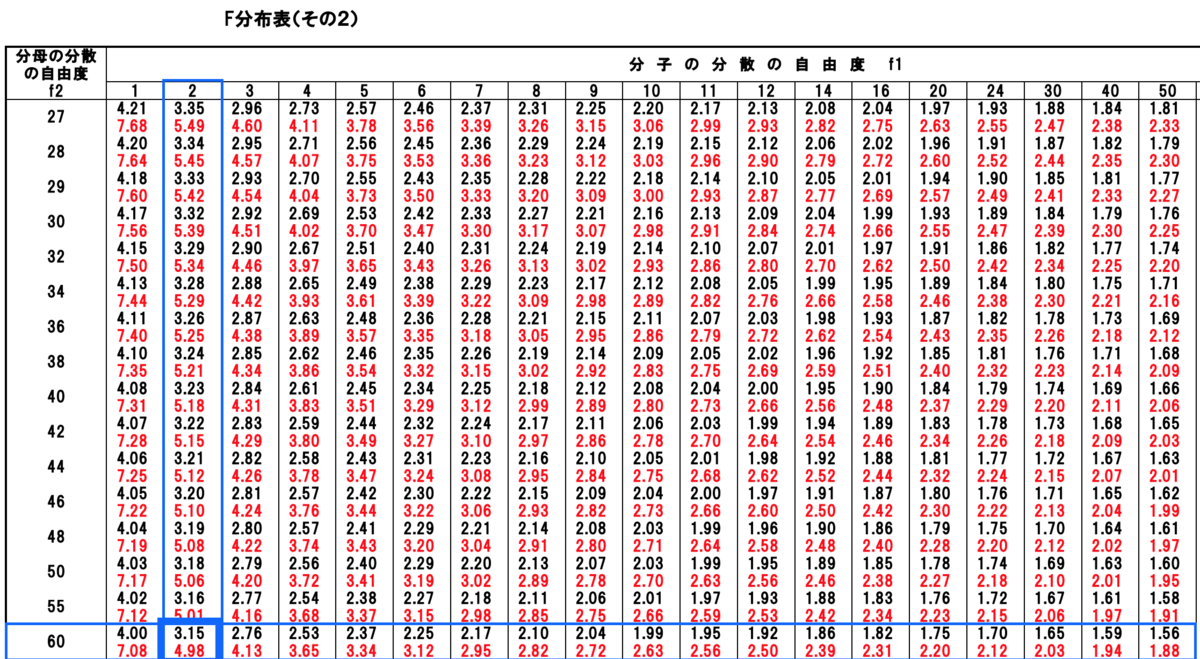
見方としては、横軸が分子の分散の自由度、縦軸が分母の分散の自由度になる。
今回は群間÷郡内でF値を計算しているので、群間が分子、郡内が分母となる。
よって、横軸が2、縦軸が57でクロスするところの数値を読めば良い。ちょうどの数字がない場合は最も近いものを選ぶ。
有意水準5%(0.05)で「3.15」と読み取ることができた。
今回計算したF値12.22は3.15より大きいため、有意水準5%で棄却域に入る。つまり帰無仮説(=「3つのお店のポテトの評価(母集団)の平均に差はない」)は棄却され、対立仮説が採択される。
有意水準1%で検定をしたとしても、12.22 > 4.98であり、同様の結果となる。
注意)対立仮説「3つのお店のポテトの評価(母集団)の平均の少なくとも1つの組み合わせに差がある」が検定の結果わかったが、あくまで”いずれかの組み合わせ”であって、”どの店とどの店の間に差がある”のかまではわかっていないことに気を付ける。
