↑勉強中のテキスト。第5章「もっと詳しく調べたい! - t検定(対応あり)」
p116 確認テスト
◆問題
ある小学校で、算数の分数の計算を教えるためのマンガを使った新しい方法を開発した。はたしてこの方法に効果があるのかどうかを確かめたい。
以前、2クラスにそれぞれ新しい方法と従来の方法で教えた後、テストを行ったところ、両クラスの平均得点の間には有意水準5%で有意な差はなかった。
そこで今回は、柳組1クラスの生徒18人に次のようなテストを実施した。分数の授業が終わったところでテストをした(事前テスト)。その後、マンガを使った分数の授業を行い、その後もう一度テストをした(事後テスト)。テストの点数データ(10点満点)は以下のようになった。これを対応のあるt検定によって分析したい。

1.この検定での帰無仮説を言いなさい
2.この検定での対立仮説を言いなさい
3.t値を求めなさい(小数点第3位を四捨五入)
4.有意水準を1%としたとき、このt値から言えることは何か
標本平均を計算すると、事前テストは8.72で事後テストは9.06であった。
事後テストの方が平均得点が上がっているが、これは教え方による有意な差があるといえるのか、もしくはデータのばらつきの範囲内であるのかを検定によって確認する。
◆解答
帰無仮説:「事前テストと事後テストによる得点の差はない」
対立仮説:「事前テストと事後テストによる得点の差はある」
それではさっそくt値の計算をしていく。今回は対応のあるt検定(テストを行った生徒が同じ→母集団が1つ)なので、まずは事前テストと事後テストの得点の「差」を計算する。エクセルで隣の列に「差」を作った。

生徒番号1~18の事前と事後による差が計算された。得点の差の平均をK21セルで計算し、-0.33となった。
不偏分散については便利なエクセル関数VAR.Sを使って一発で算出した。
サンプルサイズは例のエクセルではCOUNT関数を使って数えているが、ここは手入力でも構わない。
そして、差の標準誤差については、以下の式で計算する。
差の標準誤差 =
ここまで来ると、あとはt値を計算すれば良い。
t =標本平均÷差の標準誤差
=-0.33÷0.27=-1.24
t値が-1.24であることがわかった。t分布表からこれがどのくらいの確率で起きることなのかを確認する。
自由度はサンプルサイズ(今回は18)-1=17である。有意水準1%(α=0.01)で検定する場合は、下のt分布表から17と0.01がクロスする部分を読み取る。
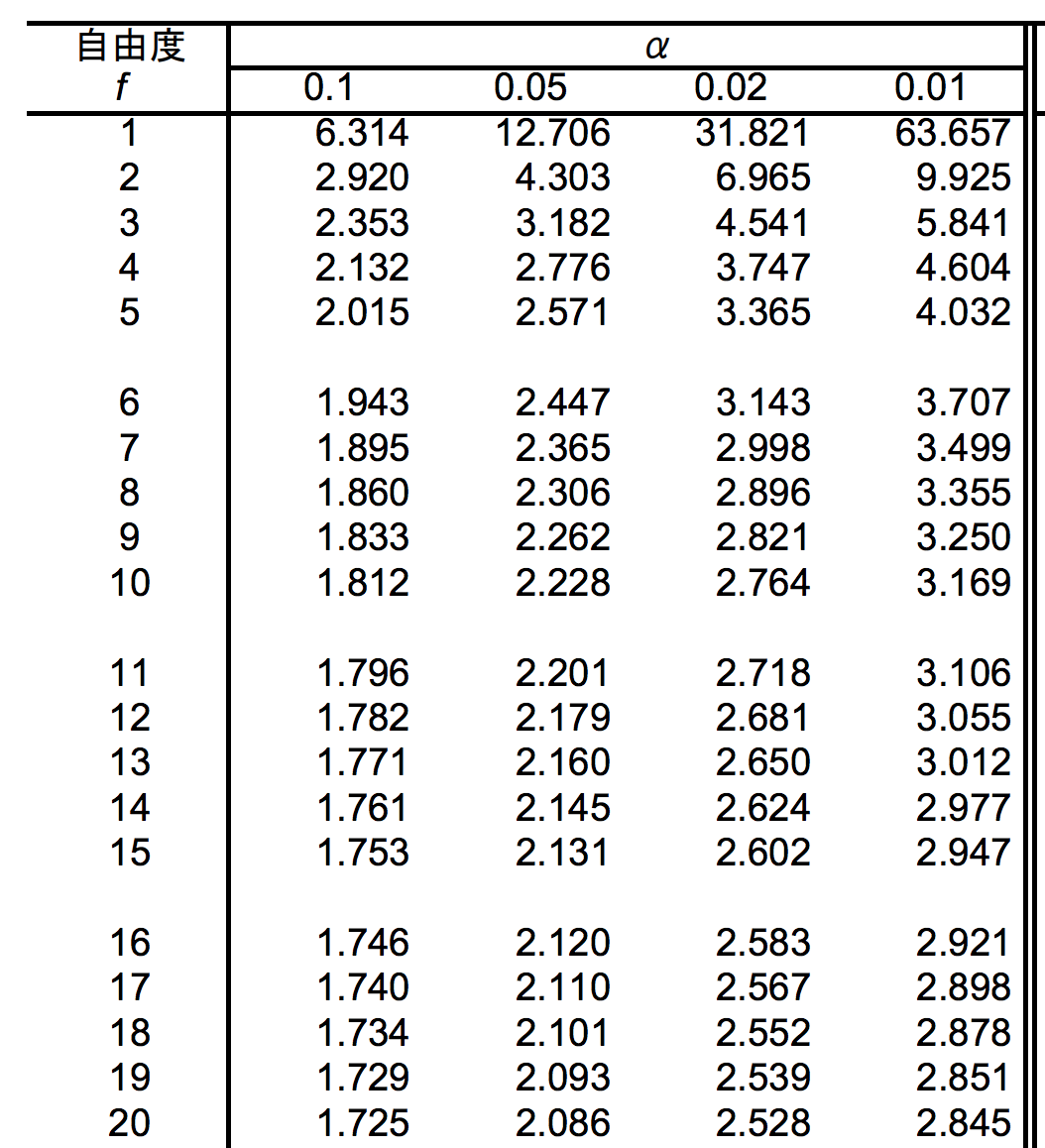
2.898と読み取ることができる。
今回計算したt値は「-1.24」であり、有意水準1%の-2.898 ~ 2.898の範囲内にあり、棄却域には入っていないため、帰無仮説を棄却できない。
つまり、帰無仮説は採択されるので、「事前テストと事後テストによる得点の差はない」といえる。(=マンガを使った分数の授業に教育効果はあるといえない)
対応のないt検定の方の練習問題はコチラ↓
