エクセルで度数分布(ヒストグラム)を作成する方法
データは『統計学がわかる』p15,第1章「ポテトの長さは揃ってる?」を参考にした。
モグモグバーガーとワクワクバーガー、2つのお店の”ポテトの長さ”をエクセルに入力する。
サンプルサイズは各49個で、特性値は「長さ」なので単位はcmとなる。
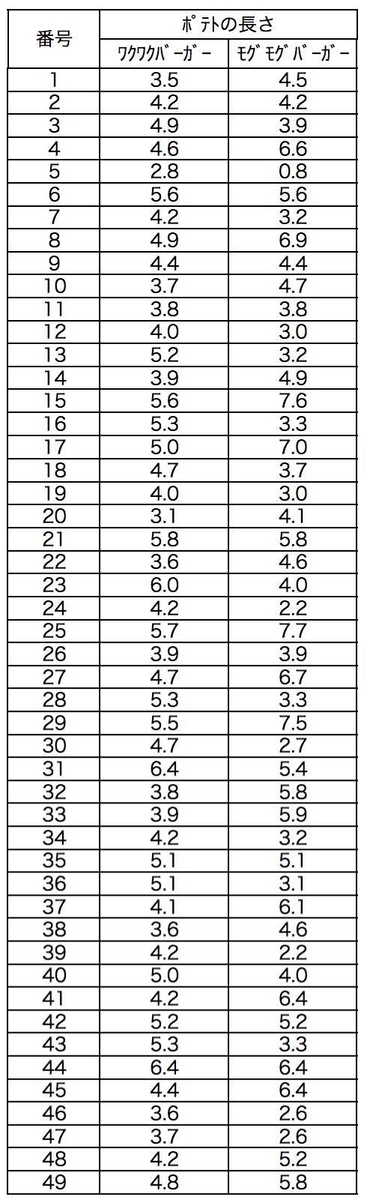
ポテトの平均長さをエクセルのAVERAGE関数を使って計算すると、
ワクワクバーガー 4.571cm
モグモグバーガー 4.614cm
で、差は4.614-4.571=0.043cmとなった。
2つのお店のポテトの長さに差はあるのか?
上の表では、ただの数字の羅列で、データの特性や違いの有無が一見しただけで判別できないため、もう少し視覚的にわかりやすく整理してみる。
その1 範囲(レンジ)を比較する
*範囲(レンジ)・・・データの持つ幅で、データの最大値と最小値の差のこと
範囲(レンジ)=最大値ー最小値
これを計算してみると、
ワクワクバーガー 6.4-2.8=3.6
モグモグバーガー 7.7-0.8=6.9 となりモグモグバーガーの方がデータの持つ幅が広く、範囲の小さいワクワクバーガーのポテトの方が長さが安定している。
ただし「範囲」は、データに外れ値が一つでもあると結果に大きく影響を受けるので注意が必要。
次に、すべてのデータの大小を一覧で比較するために度数分布を作ってみる。
その2 度数分布(ヒストグラム)の作成
度数分布(ヒストグラム)とは・・・
度数分布(どすうぶんぷ、Frequency Distribution)は、統計において標本として得たある変量の値のリストである。 量の大小の順で並べ、各数値が現われた個数を表示する表(度数分布表)で示す。 日本工業規格では、「特性値と,その度数または相対度数との関係を観測したもの」と定義している。 -Wikipedia
ワクワクバーガーとモグモグバーガーの度数分布(ヒストグラム)をエクセルで作ってみる。
データの区切りとなるグループを階級、1つの階級に含まれるデータの個数を度数と呼ぶ。
エクセルでの計算は「COUNTIF関数」を使う。
COUNTIF(範囲,検索条件)
例えば今回の例でポテトの長さが4cm以上、5cm未満の個数を数える場合、エクセルでセルには次のように入力する。
「=COUNTIF(C$6:C$54,">=4")-COUNTIF(C$6:C$54,">=5")」
上記の内、 C$6:C$54はデータの検索範囲なのでそれぞれのエクセルシートによって、
対象のデータが記載されたセル位置に修正する必要がある。
5cm未満の個数だからといって、(C$6:C$54,">=5")←のイコールを削除しないよう注意したい。
一見ここのイコールがあると5cm以下となって間違いのような気がするが、今回の場合はイコールが必要だ。
例えば、4.0cm、4.5cm、5.0cmという3つのデータがあったとして、
COUNTIF(範囲,">=4") ・・・ 範囲から4cm以上の個数(例では3個)
COUNTIF(範囲,">=5") ・・・ 範囲から5cm以上の個数(例では「5.0cm」の1個)
よって、3-1=2個となり、「4.0cmと4.5cm」の2個と合致する。
もし、ここで
COUNTIF(範囲,">5")とイコールをなしにすると、5cmを超えるもの(※5.0cmは含まない)は0個なので、3-0=3個と誤ってしまう。
さて、説明が長くなったが、ワクワクバーガーとモグモグバーガーのデータを階級と度数に分類すると以下のようになった。
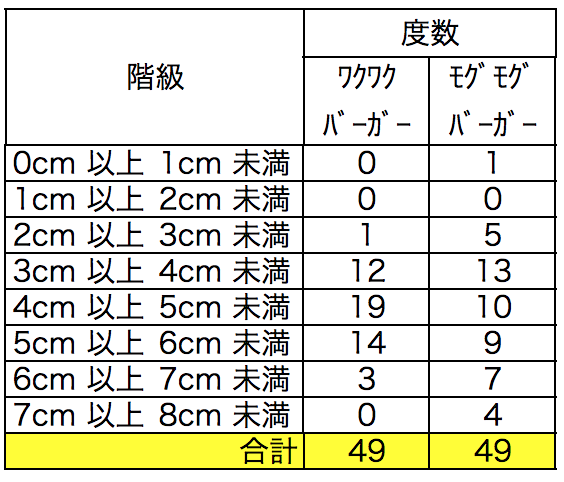
これを横軸:階級、縦軸:度数を取ってグラフ化したのがヒストグラムとなる。
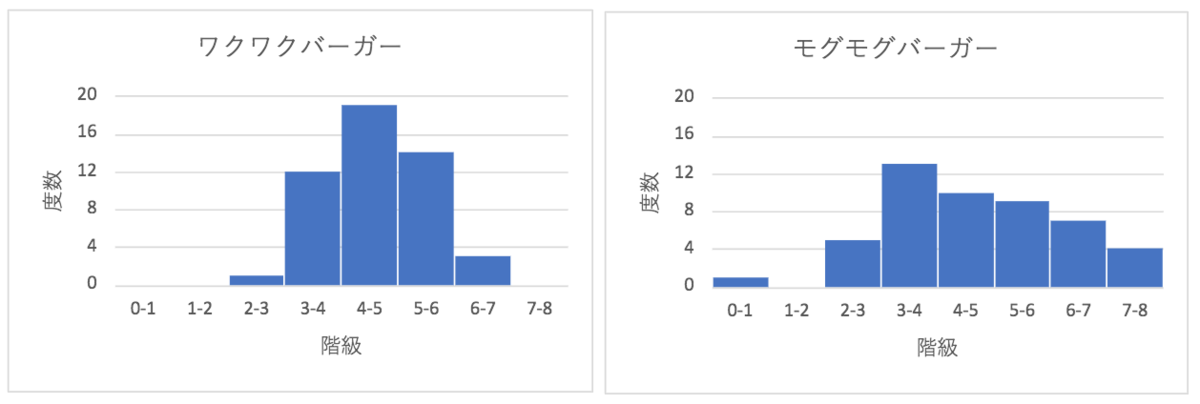
↑のグラフでは縦軸の度数にポテトの本数をそのまま使っているが、この場合サンプル数が増えると度数も大きくなるので、これを全データ数で割って、全体に占める比率とする方法もある。
全体に占める比率に直したヒストグラムが以下だ。

データの表現の仕方を変えただけで、実験データそのものが変わった訳ではないので当然ながら分布の形は同じとなる。度数をどちらで表現するかは用途に応じて使い分けると良い。
さて、ポテトの例題に戻って、度数分布(ヒストグラム)にしてみると、データの特徴が視覚的にわかりやすくなる。
ワクワクバーガーのポテトでは、最も度数が大きいのが4cm以上5cm未満の階級でこれは先に計算した平均値4.571cmとも合致する。
一方、モグモグバーガーでは、最も度数が大きいのが3cm以上4cm未満の階級だが、先に計算した平均値4.614cmとは合わない結果となった。階級の全域に広く分布しており、それだけデータのばらつきが大きいことがわかる。ここで言うデータのばらつきとは、すなわち品質のムラを意味する。
