↑勉強中のテキスト。第4章「どちらの商品がウケていますか? - t検定(対応なし)」
p98確認テスト
◆問題
ある小学校で、算数の分数の計算を教えるためのマンガを使った新しい方法を開発した。はたしてこの方法に効果があるのかどうかを確かめたい。そこで、桜組では従来通りの教え方をし、一方、桃組では新しい教え方をした。その後に、共通のテストを行った。テストの点数データ(10点満点)は以下のようになった。これをt検定によって分析したい。
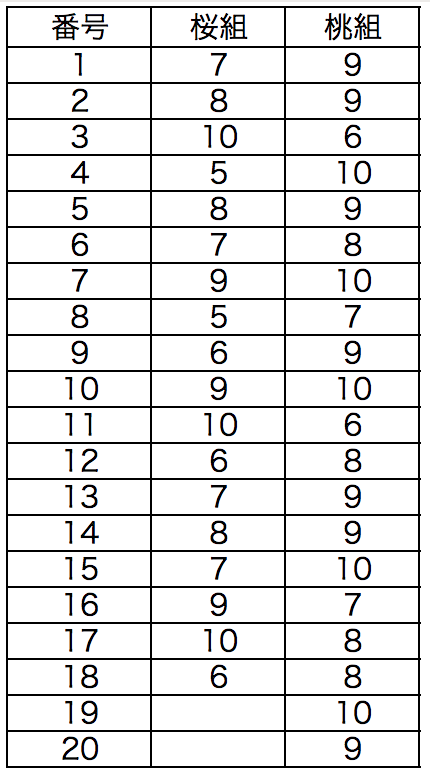
1.この検定での帰無仮説を言いなさい
2.この検定での対立仮説を言いなさい
3.t値を求めなさい
4.有意水準1%としたき、このt値から言えることを書きなさい
◆解答
帰無仮説:「従来通りの教え方と、新しい教え方によるテストの結果に差がない」
対立仮説:「従来通りの教え方と、新しい教え方によるテストの結果に差がある」
t値の計算は以下の手順で行った。桜組と桃組の標本平均と不偏分散を求める。
「標本平均の差」は7.61-8.55=-0.94とした。
(※これを逆に8.55-7.61=+0.94と計算しても以降のt検定で同じ結果となる)
差の標準誤差= なので、

t値は-0.94÷0.48=-1.95である。
また、自由度は(18-1)+(20-1)=36となる。
t分布表から自由度36、有意水準1%(0.01)がクロスするところを読み取ると、2.719である。
計算で求めたtは-1.95であり、有意水準1%(-2.719〜2.719の範囲内にあり)で棄却域には入らず、帰無仮説は棄却されない。つまり、帰無仮説は採択された。
t検定の結果、従来通りの教え方と、新しい教え方によるテストの結果に差がないことがわかった。
