↑勉強中のテキスト。第4章「どちらの商品がウケていますか? - t検定(対応なし)」
ワクワクバーガーとモグモグバーガーの味を評価した結果を以下に示す。
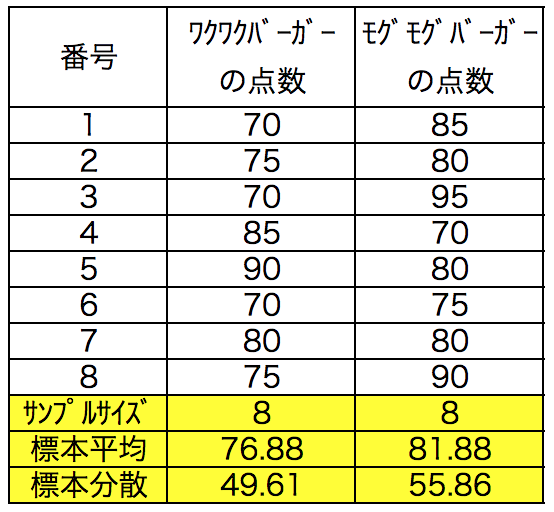
標本平均の差は81.88-76.88=5.0で、モグモグバーガーの方が5点高い結果となった。
この5点の差に意味があるのか、それともデータのばらつきの範囲内であり5点の差に意味はないのか、どちらの考えが正しいのかをt検定で確認する。
今回の例ではワクワクバーガーとモグモグバーガーの味の評価を別々の人が行ったので、対応のないt検定を用いる。対応のないとは、独立した別個の母集団であることを意味する。
平均値の差の信頼区間を計算する
母集団Aから抽出した標本平均Aと、母集団Bから抽出した標本平均Bの差の分布は、正規分布に従うので、母平均の信頼区間を求める式をそのまま使うことができる。
平均の差の信頼区間は以下の式で計算する。
平均の差の信頼区間=(標本平均A-標本平均B)±t x 差の標準誤差
また、差の標準誤差については以下の式で計算する。
差の標準誤差=
注)テキストでは、ここからさらに式を発展させて推定母分散を用いているが、本ページでは推定母分散は使わずに以降も上記の式で計算を行っていく。
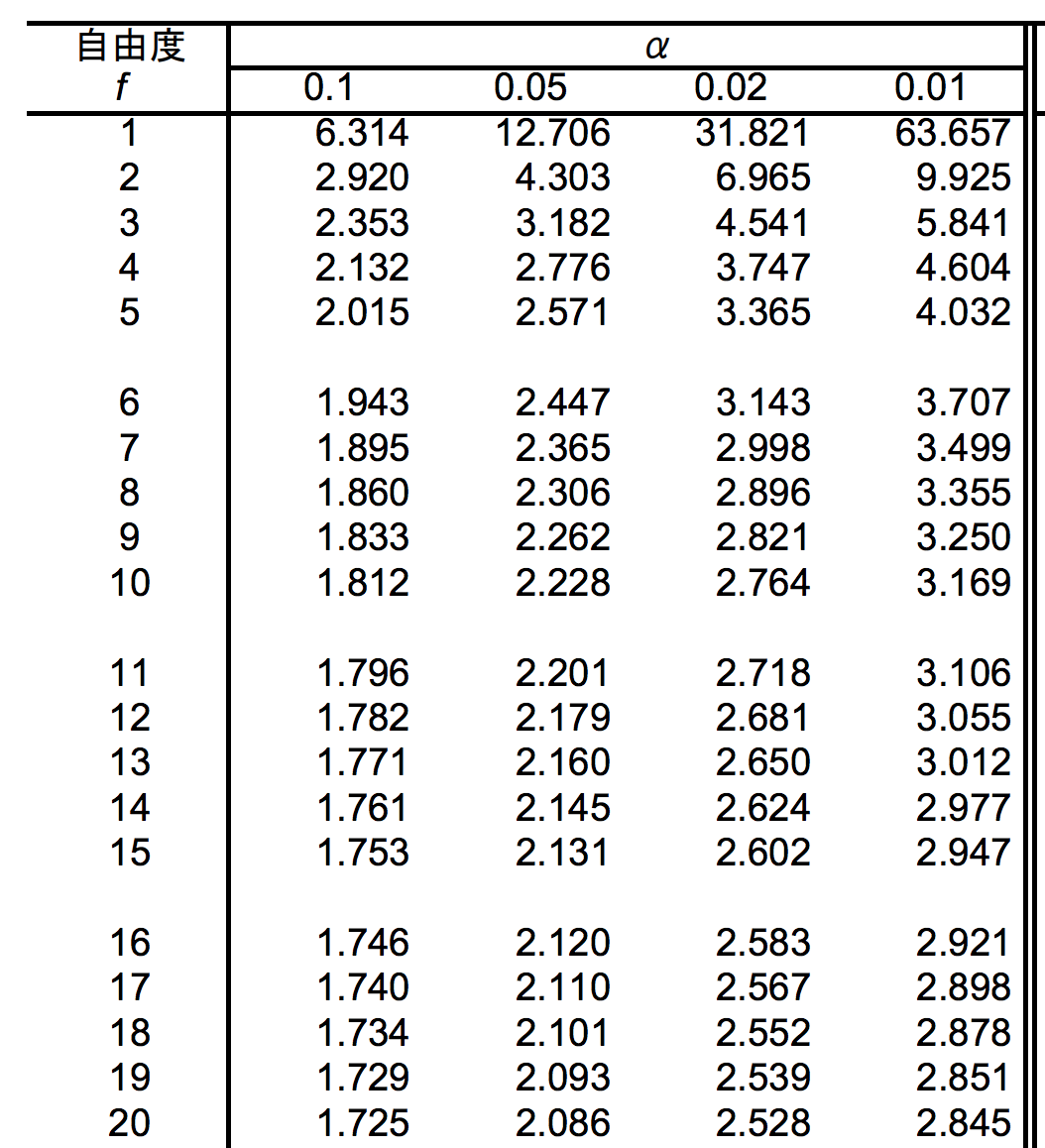
自由度は(8-1)+(8-1)=14である。
t分布表より自由度14のときの有意水準5%(α=0.05)は、表からクロスするところを読み取ってt=2.145となる。
ここまでわかったので、平均の差の信頼区間を計算する。結果を以下に示す。
「差の標準誤差」の計算で、標本分散ではなく、不偏分散をサンプルサイズで割ることに注意したい。セルに入力した計算式をオレンジ色の文字にしている。
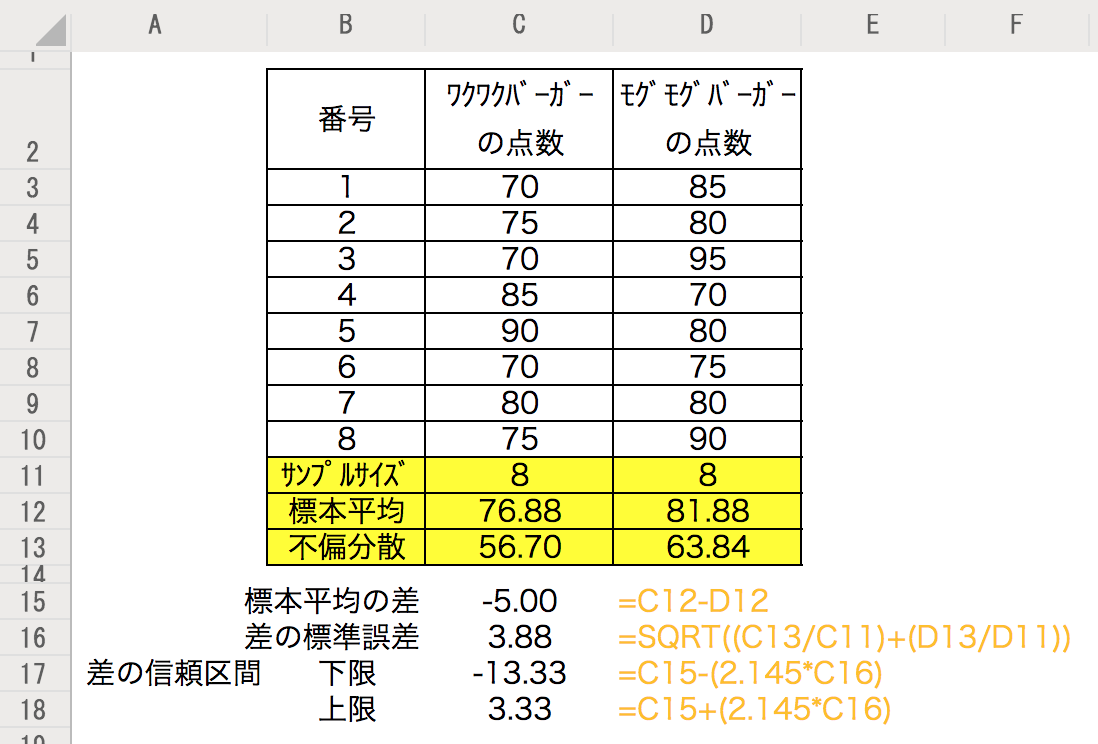
差の信頼区間はt=2.145を用いて、-13.33から3.33の範囲ということがわかった。
つまり、この範囲内に母集団の平均の差が含まれる確率は95%だということだ。
t検定を使って仮説検定をする
2つ店の味の評価に差があるかを検定する。
帰無仮説は、「ワクワクバーガーとモグモグバーガーの味の評価に差はない」となる。
tは以下の計算式で求める。
t = 標本平均の差 ÷ 標本平均の差の標準誤差
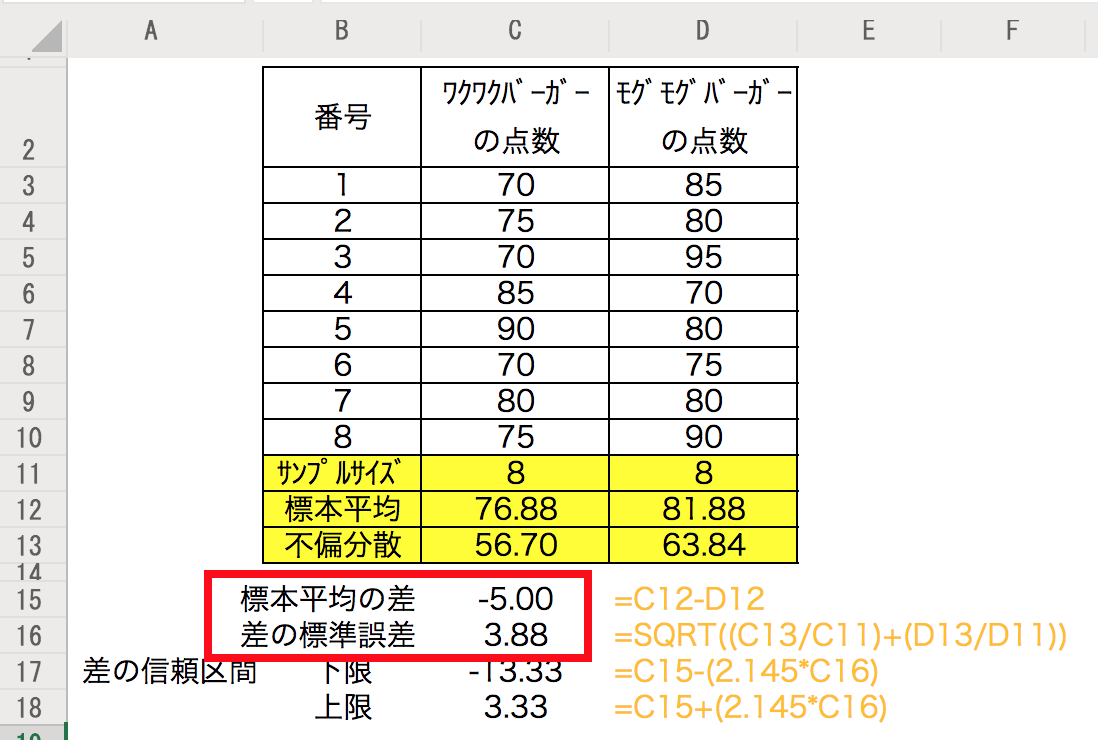
赤枠で示したところの数値を使って計算すると、
t=-5.00 ÷ 3.88=-1.29となる。
あとはこの「-1.29」をt分布表と見比べて、統計的に差があるといえるかどうかを確認すれば良い。自由度は今回の場合、2つの店のサンプルサイズが8だったので、
(8-1)+(8-1)=14である。

t分布表から、自由度14と有意水準5%(α0.05)がクロスするところを読むと、
2.145となる。これは次のことを意味している。
自由度14のとき、tが2.145よりも大きい、または-2.145よりも小さいことが起こる確率は5%未満である。
上の計算例では、標本平均の差の計算をワクワクバーガー - モグモグバーガーで行ったが、これを逆にして計算すると、t=1.29と符号が反転するためt分布表から読み取った値と比較するときは、-2.145から+2.145の範囲より外にあるか、内にあるか、で考えるようにするとミスをなくせる。
さて、いよいよ今回の結果だが、計算したt=-1.29は5%有意水準(-2.145〜+2.145の範囲内にあり)での棄却域に入らない。よって、帰無仮説は棄却できず、「ワクワクバーガーとモグモグバーガーの味の評価に差はない」と結論付けられる。
