↑勉強中のテキスト。第5章「もっと詳しく調べたい! - t検定(対応あり)」
そもそも、「対応のある」「対応のない」とは?
t検定の話に入る前に、まず「対応のあるt検定」や「対応のないt検定」と言うとき、この「対応」とは一体何かを確認しよう。
対応のある、ないとは要は母集団が独立しているかどうかと考えて相違ない。
このテキストの例では、ワクワクバーガーとモグモグバーガーの味の評価を女子高生に協力してもらったが、採点する女子高生で仮にA~Eの5人がワクワクバーガーを、F~Jの5人がモグモグバーガーの評価をしたような場合は「対応のないt検定」ということになる。第4章ではこっちのパターンだった。これは、もしハンバーガーなどのジャングフードを元々好きな人がたまたま多くなったりしたら、それだけで本来の店の味以上に点数が良くなったりする可能性を持っているということだ。
一方、女子高生A~Eの同じ5人にワクワクバーガーとモグモグバーガーを両方食べ比べて採点をしてもらう場合などは「対応のあるt検定」ということになる。
こちらで実験をする場合は、先に食べる方と後に食べる方をランダム化させることに注意が必要だ。
対応のあるt検定をやってみる
さて、前置きは以上で、テキストに戻ることにする。
女子高生8人に2種類のハンバーガーを食べて比較した結果を以下に示す。
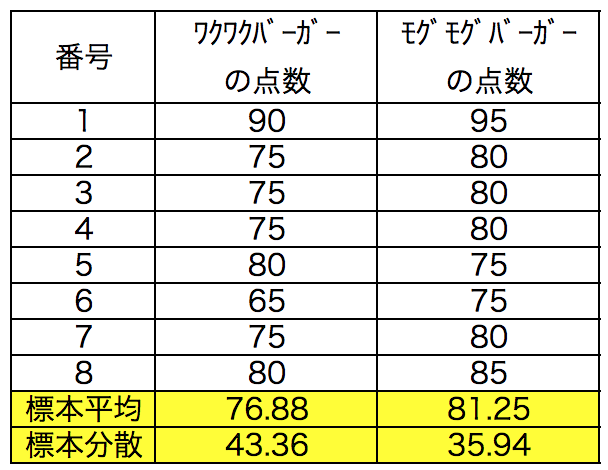
標本平均は76.88-81.25=-4.38となり、モグモグバーガーの味の評価の方が4.38点だけ高いという結果だ。これが有意な差であり、実際にモグモグバーガーの方が味が勝るのかを検定でみていく。
対応のないt検定のときは「2つの独立した母集団から標本を選んでくる」という条件で、
今回の対応のあるt検定のときは「1つの母集団から標本を選んでくる」という条件だ。
では、このときの1つの母集団とは何か?それはワクワクバーガーとモグモグバーガーの評価の差のことだ。
「ワクワクバーガーの点数」-「モグモグバーガーの点数」で「点数の差」列を追加した。
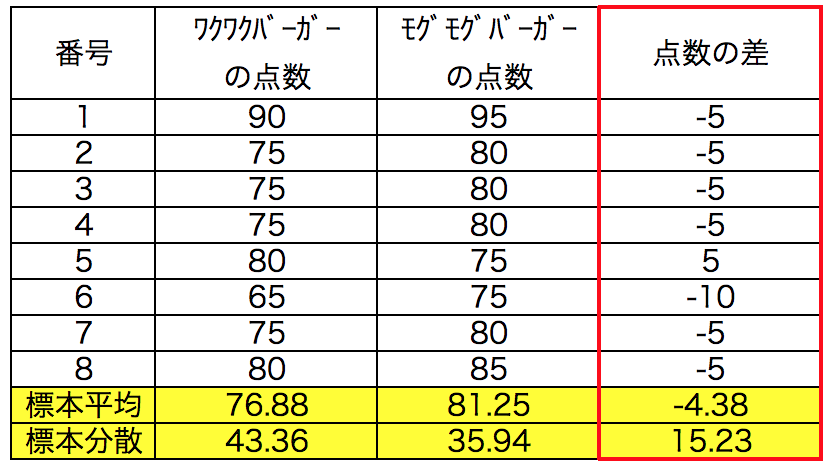
点数の差は、平均が-4.38、分散が15.23となった。この点数の差は意味があるのか?
tは以下の式で計算する。
t = 差の平均÷差の標準誤差
そして、差の標準誤差は、以下の式で計算する。
差の標準誤差 =
これらを踏まえて、先ほどの表の計算を進める。点数の差についてのみ計算を追加した。
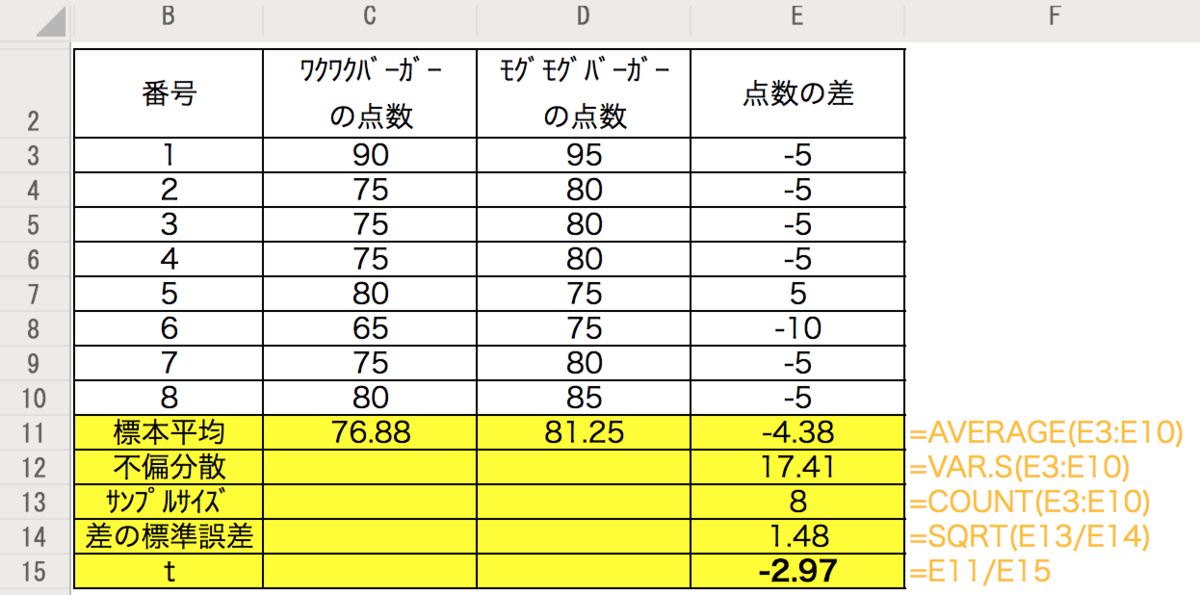
オレンジ色の文字でセルに入力した数式を示した。
tは、標本平均-4.38÷差の標準誤差1.48= -2.97となった。
ここまで来れば、あとはt分布表を見てこの-2.97がどのくらいの確率で起こるのを確認すれば良い。
t分布表を以下に示す。自由度はサンプルサイズ(8)-1=7である。
有意水準5%(α=0.05)がクロスするところを読み取ると、「2.365」である。
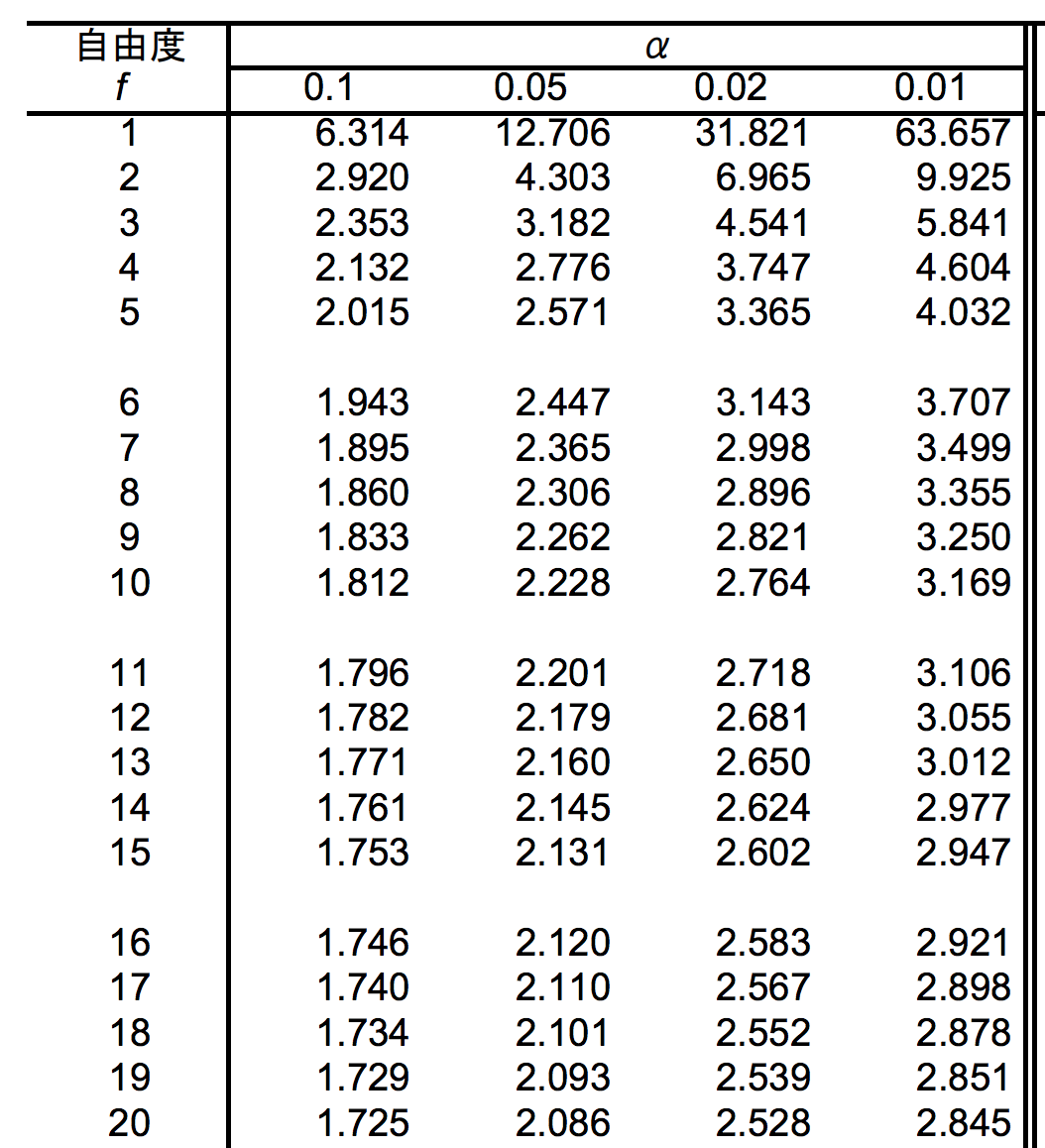
t分布表から有意水準5%で-2.365 ~ 2.365であり、今回計算したtは-2.97でそれよりも大きいので、帰無仮説は棄却され、対立仮説が採択される。
つまり、「ワクワクバーガーとモグモグバーガーの味の評価には差がある」(=「ない」とは言えない)ということになる。
ちなみに、これまで見てきた例で有意水準5%では検定の結果、有意な差があると結論付いたが、では有意水準1%ではどうだろうか。
先ほどのt分布表から有意水準1%(α=0.01)と自由度7がクロスするところを読むと、3.499となっている。
つまり、有意水準1%ではtが-3.499 ~ 3.499であり、今回計算したt値は-2.97でありこの範囲内にあるので帰無仮説を棄却できない。
よって、「ワクワクバーガーとモグモグバーガーの味の評価には差はない」と有意水準5%とは反対の検定結果となる。いまいち腑に落ちない部分があるが、つまりは今回の例のようなことが起こる確率は1%以上5%以下ということだ。
対応のないt検定と対応のあるt検定の違いについて
差の標準誤差の計算式は以下のような違いがある。
対応のないt検定での差の標準誤差
差の標準誤差=
対応のあるt検定での差の標準誤差
差の標準誤差 =
√(不偏分散÷サンプルサイズ)
式を比べてわかるように、対応のあるt検定の方が母集団が1つであるために差の標準誤差が小さくなる傾向がある。差の標準誤差が小さくなるということは、信頼区間の幅が狭くなり、より真の値の推測に近づけるということだ。
よって、対応のあるt検定の方が、有意な差を見出す検出力が大きくなることは覚えておきたい。
対応のないt検定の復習はコチラ↓
