直交配列表とは
直交表とは、任意の因子について、その水準のすべての組合せが同数回ずつ現れるという性質をもつ実験のための割り付け表である。
一般に要因配置型の実験では、少なくとも因子の水準数の積の回数だけ実験数が必要になり、因子数が多くなると実験回数は膨大な数になってしまうという欠点がある。
求める交互作用が少なければ、直交表を用いることによって多くの因子に関する実験を比較的少ない回数で実施することができる。
3水準系の直交配列表はこんな時に使う:2水準系との違い
3水準系の直交配列表は、一つの列の係数が1、2、3からなり、3水準の因子の実験に用いられる。3水準にすると実験回数は増えるものの、水準の設定範囲内で効率的に最適水準を見つけやすくなるメリットがある。
3水準系の直交配列表実験は以下のような時に計画する。
・水準の設定範囲内で特性が1次式的な傾向を示さないと予想される場合
・水準の値の方向性が不明で、水準を大きくすべきか小さくすべきかが分からない場合
・ある条件を挟んだ両側で実験をしたい場合
 表記について
表記について
3水準系の直交配列表はと表記される。
直交配列表を表すLは、直交配列表のもととなるラテン方格(Latin Square)の頭文字、Nは行数を表し、1行が1つの実験なので、つまりNは実施する実験回数となる。また、このNを直交配列表の大きさと呼ぶ。
mは列の数を表す。3水準系では全体の自由度がN-1であり、1列の自由度が3-1=2なので、列の数mは(N-1)/2となる。
列には要因(主効果、交互作用、誤差)を割り付ける。
◆直交配列表

◆直交配列表

3水準系直交配列表について、例えば上記の表には13個の列があるが、隣り合うどの2列を見ても 、
(1,1)(1,2)(1,3)
(2,1)(2,2)(2,3)
(3,1)(3,2)(3,3)は同じ回数だけ現れる。
さらに大きな3水準系直交配列表として、も一応存在するが実験回数が多くなりすぎ、一部実施法と交絡法を応用した直交配列表実験の特性がほとんど活かせないので一般的ではない。
実験の計画について
実験の計画とは、知りたい要因(主効果、交互作用、誤差)を直交配列表のどの列に割り付けて実験を実施するかを決めることである。
直交配列表の各列の係数は1、2、3なので、各列が持つ自由度は2である。
3水準の因子の自由度は、(3-1)=2なので、1つの列に1つの因子を割り付ければ良い。
次に3水準の因子同士の交互作用は、(3-1)x(3-1)=4なので、交互作用を割り付けるには2つの列が必要である。(1つの列が持つ自由度は2しかないため)
ここの部分の考え方は2水準系の直交配列表と異なる。
また、直交配列表で実験を計画する時の注意点として、主効果も交互作用も割り付けていない列を「誤差列」として最低1列は確保しておく必要がある。
誤差列からは、実験誤差の大きさを推定することができ、効果を知りたい要因が交絡していないことを確認する。
割り付けをする方法は以下の2つがある。
1.線点図を用いる方法
2.成分記号を用いる方法
上記の内、線点図の方が扱いやすいので以降の例題は1のパターンのみについて確認していく。
線点図による実験の計画
線点図は要因効果の割り付けを視覚的に分かりやすくしたもので、因子を点で、交互作用を線で表す。直交配列表の大きさによって、あらかじめ用意された何パターンかの線点図があるので、それを部分的に改変して使う。
の線点図

の線点図

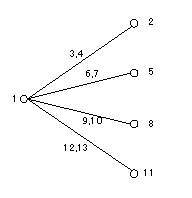
の線点図


◆参考
2水準系の直交配列表実験については以下の記事をご参照ください。
