工程能力および工程能力指数とは
工程能力（Process Capability）は、製造プロセスやビジネスプロセスが設計要件や仕様にどの程度合致し、安定した品質を提供できるかを評価するための指標や概念のこと。
もう少し簡単に言い換えると、
工程能力とは、”定められた規格の範囲内で製品を生産できる能力”のこと。
そして、その評価を行う指標を工程能力指数という。
工程能力指数（CpおよびCpk）は、製造またはビジネスプロセスのパフォーマンスと品質を評価するために使用される統計的指標のことで、
これらの指標は、製造プロセスが製品仕様内でどれだけうまく動作しているかを評価するために使用される。
工程能力指数Cpとは
Cpは、製造プロセスの変動と製品仕様の許容範囲との関係を示す指標である。
Cpが高いほどプロセスが安定していると考えられ、製品の品質が良いと判断される。
Cpが1より大きい場合、プロセスは仕様内に収まると考えらる。しかし、これはプロセスが中心に配置されているかどうかを考慮していない。
Cpの計算方法は、検討対象の規格が両側か片側かで以下のように計算する。
◆両側規格の場合
◆片側規格の場合
上限の規格の場合
下限の規格の場合
まずは、一般的な両側規格のCpについて、例をいくつかあげて計算する。
ある工場で生産している製品の長さが規格上限:13cm、規格下限:7cmであったとする。
現場での狙い値は中央の10cmで加工している。
例1)長さの平均値10cm、標準偏差0.5cmの工程
エクセルでNORM.DIST関数を使って確率密度の正規分布曲線を描いた。
両側の規格に対して生産した製品の長さが、ばらつきを含めても十分規格内であり、工程能力指数Cpを計算すると、
となり、十分過ぎるくらい高い水準で管理された工程であることがわかる。
実際にこの工程で不良品（＝長さが規格外）が発生する確率を計算すると「0.000000044%」である。
例2)長さの平均値10cm、標準偏差1.5cmの工程
次のパターンでは、製品の平均値こそ中央の10cmで管理できているものの、標準偏差（≒データのばらつき）が大きいので、工程の状態は悪い。
であり、不良品の発生確率は3.86%と高い。ばらつきが大きいために不良のムダが多いパターンだ。
例3)長さの平均値12cm、標準偏差0.5cmの工程
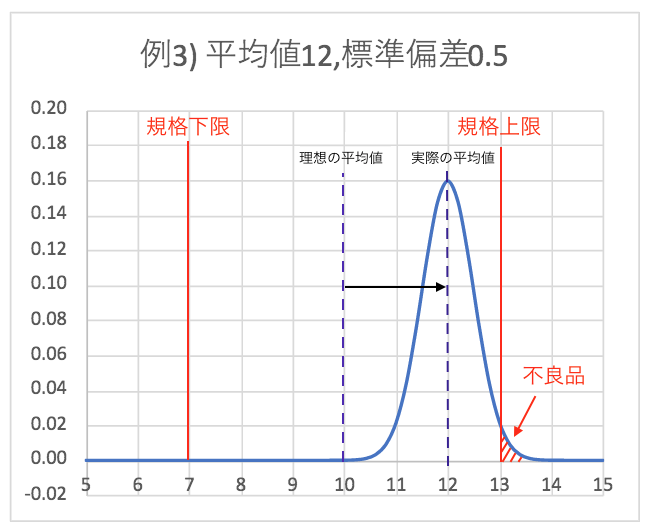
3つ目のパターンは、標準偏差は小さく抑えられているが、平均値が本来の狙いよりもズレた状態の工程だ。
平均値が規格上限側にシフトしているため、図の赤斜線部で示した部分の面積が不良品となる。
工程の状態としては良くないのだが、Cpを計算すると
となり十分過ぎる程管理された工程という結果になるが、何かおかしい。
不良品の発生確率（赤斜線部の面積）を計算すると、1.34%となり例1に比べても格段に高い。
Cpの計算では、規格の幅と標準偏差のみを用いるため、工程でつくられる製品の平均値は必ず規格の中央にコントロールできていることが前提になっている。
例3のように平均値が中央でない場合は、偏り（かたより）を考慮したCpkで計算する。
工程能力性能指数Cpkとは
Cpkとは、製品特性の平均値が規格の中心値よりどれだけずれているかを考慮したものである。
Cp工程能力指数と区別するため、Cpkは工程能力性能指数と表現されることもある。
製造メーカなど実際の工程では「Cpk」を使う場面が圧倒的に多い。
実際に試作段階や量産で工程能力を評価したい時、評価前の状態では平均値が中央でコントロールされているか不明な場合が多いので、中心からのずれを補正するCpkを計算する方が早い。
Cpkの計算には以下の2つの方法がある。
１．片側規格のCp(上限/下限)をそれぞれ求め、小さい値をCpkとする。
２．データの偏りを示すKを計算し、Cpから計算する。
それぞれの計算方法を先ほどの例3を使って確認してみる。
１．片側規格のCp(上限/下限)をそれぞれ求め、小さい値をCpkとする。
上限規格
下限規格
よって、両者比較で小さい方を採用するのでCpk=0.67
２．データの偏りを示すKを計算し、Cpから計算する。
となり、どちらの計算方法でもCpkは同じであることが確認できた。
個人的にはパターン1の方が断然使いやすいと思っている。
工程能力指数の判断基準
工程能力指数（Cp,Cpk）で工程の状態を判断する時の一般的な目安は以下。
業界や対象の製品によって若干異なる部分（例えば安全を非常に重視している）はあるが、多くは工程能力指数「1.33」を目標値にしている。
理想的には高ければ高いほど望ましいが、コストとのバランスとなる。
それぞれの工程能力で実際の不良品の発生確率がどの程度かも示しておく。
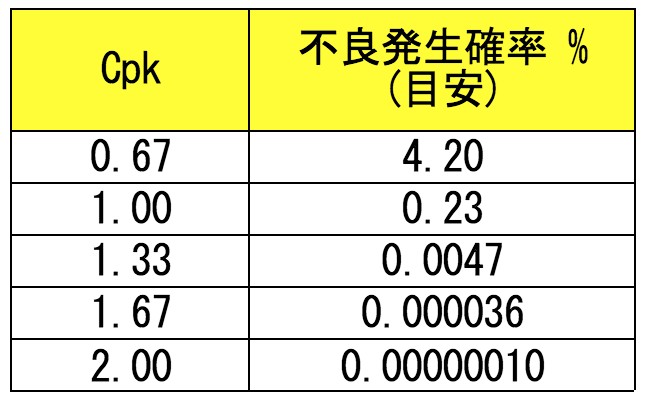
確率的にもCpk=1.33というのが現実的な落としどころになるというのがわかる。
Cp,Cpkの違いを整理
・Cpはプロセスの変動が仕様の範囲内に収まっているかを評価する。
・Cpkはプロセスの変動と中心位置の両方を考慮して評価する。
→Cpkは、プロセスの変動だけでなく、中心位置（平均値）が目標値に対してどれだけズレているかも考慮して評価する。
→よって、プロセスの偏りや調整の必要性を検出することができる。
・CpとCpkの値が大きいほど、プロセスはより安定しており、品質が高いと評価される。
・CpとCpkの値が1.0あるいは1.33よりより大きい場合、プロセスは仕様の範囲内に収まっていると判断できるが、CpkがCpよりも小さい場合はプロセスに偏りがあると考えられる。
品質管理とプロセス改善
製品やサービスが一貫して仕様に適合することは、品質管理とプロセス改善の中心的な目標の一つである。
工程能力の評価は、以下の点に焦点を当てて行われる。
1. プロセスのばらつき（Variability）
プロセス内でのデータのばらつきや変動の程度を評価する。
プロセスが安定している場合、ばらつきは少なく、一貫性がある。
品質を保つためには、ばらつきを最小限に抑えることが重要である。
2. プロセスの中心（Centering the Process）
プロセスの平均値が設計仕様やターゲット値に近いかどうかを評価する。
プロセスの中心がずれている場合、品質の低下や仕様からの逸脱が発生する可能性が高まる。
上記2点の評価や検討のために使われる指標がCp，Cpkである。
↑ 工程能力，σ（標準偏差），抜取検査についてもっと詳しく知りたい方はこちら
↑ 製造業における品質管理についてもっと詳しく知りたい方はこちら
