2水準系直交配列表における「多水準法」とは?
2水準系の直交配列表実験で、特定の因子だけ4水準として実験を計画したい場合には、多水準法という割り付け方法を使う。
このような場合、2水準系直交配列表の1列の自由度は(2-1)=1であるのに対して、4水準の因子の自由度は(4-1)=3であるため、4水準の因子を割り付けるには3列が必要である。
この3列はどれでも良いのではなく、任意の2列とその交互作用列を使うというルールがある。
線点図で表すと以下のような関係になる。(両端の丸とそれを結ぶ線)

また、成分記号で表すと以下のような関係となる。(任意の因子2列とそれらの交互作用が表れる列を加えた計3列)

4水準(,
,
,
)の設定は指定した2列の係数を
(1,1)→
(1,2)→
(2,1)→
(2,2)→ とする。
2水準直交配列表実験の「基礎」については以下の記事を参照ください。
以下で、具体的な例題を用いて2水準系直交配列表実験における多水準法のStatWorks(スタットワークス)を活用した解析方法を確認していく。
[例4.5:コート紙の表面平滑度に関する直交配列表実験(4水準の因子がある場合)]-p69
プリンター印刷用コート紙の開発を行なっているが、表面の平滑度が目標に対して未達である。平滑度を向上させるコーティング条件を知るために、以下の因子と水準を取り上げて実験を行なった。

希釈量については、実験範囲内で2次的な傾向を示す可能性があるので4水準とした。
知りたい交互作用はAxBである。
特性値は表面粗さで、値は小さい方が特性として望ましい。
◆STEP1:直交配列表の大きさの選択
まずは今回の例題の系全体における自由度を計算する。
単独の因子による主効果の自由度は、水準数-1で計算できるので、
・因子A = (4-1) =3
・因子B~H = 6x(2-1) = 6 であり、
交互作用の自由度は
・交互作用AxB = (4-1) x (2-1) = 3 である。
よって、系全体の自由度は3+6+3=12となる。
では足りないので、
を使う。
は15列ある(=自由度が15)ので、今回必要な12列を割り付けても3列が余り、その余った3列は「誤差列(記号:e)」として設定する。
◆STEP2:必要な線点図の作成
知りたい要因を線点図で表現する。
割り付けを簡単にするため、用意されている線点図をベースに修正が必要な部分のみアレンジすると良い。用意されている線点図と完全に一致するのは稀であり、多くの場合は線や点を外して解析対象に沿った線点図に修正する。
コツとしては、書く順番を交互作用の検討が必要な因子から書いていく。
今回必要な線点図は、以下のようなものとなる。
(ipadに手書きしたもので見にくいのはご容赦ください)
多水準因子であるAと、それを含む交互作用AxBを優先して配置した。因子Aを緑マーカーの3箇所で、交互作用AxBも同じく自由度が3なので、ピンク色マーカーの3箇所で示した。
因子F、G、Hについては交互作用を検討する必要がないのでどこに配置しても良い。

用意されている線点図の中から、必要な線点図として先ほど書いたものに最も近い形状は以下となる。

この線点図に今回の要因を割り付けていく。割り付けた結果を以下に示す。
要因を黒字で、列番号を青字で書いている。オレンジ色の破線部は要因を何も配置していないので誤差列:eとして設定する。

◆STEP3:直交配列表への割り付け
線点図が作成できたので、列番号を参考に直交配列表に割り付ける。
因子を黒字、交互作用と誤差をグレー文字で示した。
ここで黒字になっている因子と水準に従って計16回の実験を行えば良いことになる。

スタットワークスによる解析手順
線点図の作成と直交表への割り付けイメージができたので、StatWorks(スタットワークス)を活用した解析手順に移る。
ソフトを立ち上げて、新規のワークシートを開く。
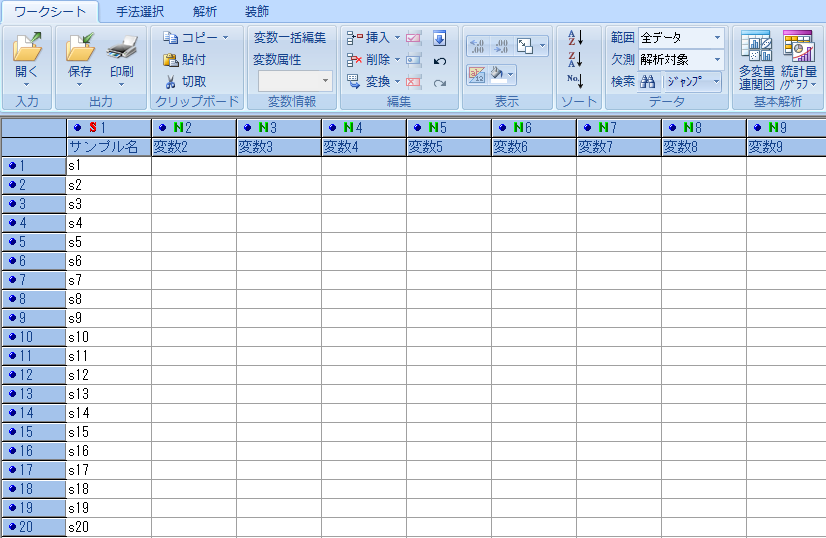
タブ「手法選択」→「実験計画法」→「直交表実験のための計画」をクリックする。
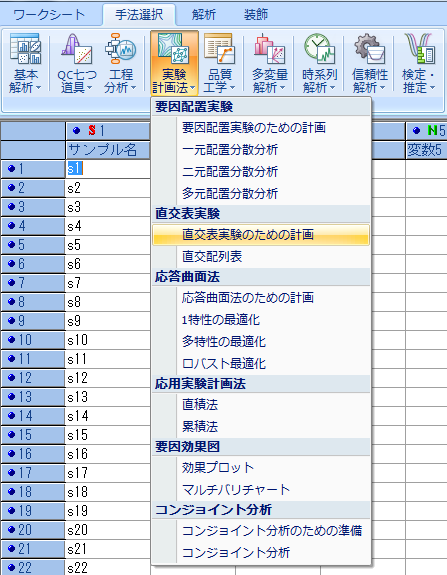
「直交表種類の選択」ウィンドウが表示されるので、事前に確認した直交表の大きさを選択する。今回は2水準系のを選べば良い。
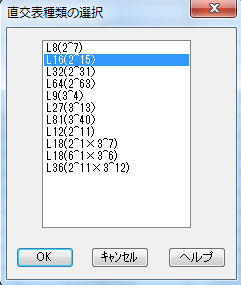
「因子の設定」ウィンドウが表示されるので、今回の実験条件(=因子)を作成していく。左上の黄色をクリックすると新規の因子がツリーに追加される。
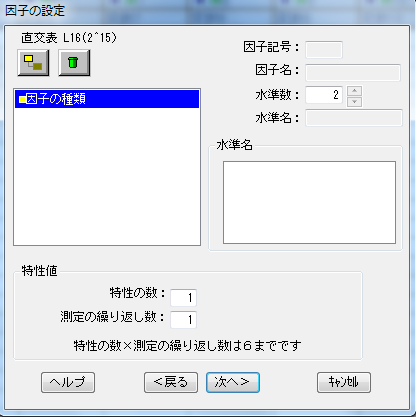
例題に沿ってA~Hの7水準を作成した。今回は因子Aだけ4水準でそれ以外は2水準である。「水準数」の「↑」or「↓」をクリックすると、任意の数を追加できる。
入力が完了したら「次へ」をクリックする。

「割り付け」ウィンドウが表示される。
直交配列表の列番号に検討したい因子と交互作用を割り付けていく。左の成分記号表を参考にするか、右側の線点図を元に割り付け作業を行う。
線点図のところで「<」「>」をクリックすると、参考となるベース線点図を確認できる。(直交配列表では、6種類ある)
今回は、事前に線点図への割り付けは済ませてあるので、画面左表の「わりつけ」列へ因子記号を書き込んでいく。

画面左表への「わりつけ」が完了した状態を以下に示す。
交互作用の表記は「AB」とする。「AxB」とするとエラーになるので注意。
また、今回の例題では11、13、15列目を誤差列として扱うが、ここは空欄にしておく必要があるのでここも注意が必要だ。
私は最初「e」と入力していたが、そうすると次のページで”わりつけが正しくありません”とエラーメッセージが出る。
スタットワークスでは、具体的にどの部分が間違っているかまで教えてくれないので、これらの入力ルールについてはよく理解しておきたい。

次に多水準法の解析では、以下のような「多水準の列指定」ウィンドウが表示されるので、今回の割り付けでは因子A(4水準,自由度3)の水準作成列は1と2である。

「わりつけ」が完了し、解析シートに実験条件一覧が表示されたことを確認する。
リボンの「4:変数への登録」をクリックすると、ワークシートへ同じ内容が転写される。
また、この頁で上部にある「表示形式 変更」を押すとA1,A2の表記が1,2と切り替わるがこれは表示だけなので適宜見やすい方にしておけば良い。

ワークシートに戻る。作成した因子、水準と割り付けが正しく行われ、実験条件一覧表が表示されている。
3~9列目は因子(実験条件)でC:質的変数となっている。10列目の表面粗さが今回の例題での特性値であり、N:量的変数となっていることを確認する。
この10列目に実験データを入力する。本来であれば、ここで実験順序をランダマイズして実験を行うSTEPに入るのだが、今回はテキストの例題を活用しているので、そのまま実験結果を入力する。

実験データの入力がすべて完了した状態が下記。
ここから、直交配列表実験における多水準法の解析に移る。

タブ「手法選択」→「実験計画法」→「直交配列表」を選択。

「変数の指定」ウィンドウが表示されるので、解析に必要な実験条件、特性値、割り付けの列番号を仕分けしていく。最初は下記図のような画面で、ワークシートで作成した列番号すべてが、画面左側の枠にすべて表示されている。
ここで「No」とは、列番号を意味している。

下記に仕分けが完了した状態を示す。
直交配列表実験では「割り付け」という列番号を指定するところが、要因配置実験とは異なる。実験条件は因子のことで、今回の例題では7個となる。
項目の仕分けがOKなら「次へ進む」をクリックで解析が実行される。

解析結果の確認
タブ「実験データ」→「データプロット」で横軸:因子の水準、縦軸:特性値の散布図プロットを確認できる。×印が実験生データ、○印が水準平均を示す。

・因子A:希釈量については、実験範囲内で2次的な傾向を示しているのがわかる。
・因子A、B、C、G、Hによる主効果が大きそうである。
・因子D、Fは効果が小さそうである。
タブ「実験データ」→「統計量」で因子の各水準ごとや交互作用の組み合わせによる平均値を確認できる。先ほどのデータプロットはこれらをグラフにしたものである。

次に「分散分析表」の確認をする。

「検定」列から因子Hは1%有意、因子AとCは5%有意であることがわかる。
有意となっていない(*が表示されていない)要因については、「分散比」と「P値」を確認し、推定の精度を高めるために効果のない要因は積極的にプーリングしていく。
注)直交配列表実験では主効果、交互作用のどちらとも効果が小さければプーリング対象とする
今回の例題では、分散日が2.0以下の因子DとFの2つをプーリング対象とする。
プーリングの基準や考え方は以下の記事にもまとめている。
プーリングをしたい要因が決まったら、その行をクリックして下のように色付きにして、リボンメニューもしくは右クリックで「プーリング」を選択する。

プーリングしたことによって分散分析表が再計算される。
具体的には、プーリングした2つの要因(因子D、F)の平方和と自由度が「誤差」に加算されることで、分散比や検定結果が変わっている。

プーリングによる再計算の結果、因子A、C、Hについては1%有意、
因子B、G、交互作用AxBついては5%有意という結果となった。
最適水準の推定
分散分析表が完成し、各要因の効果が定量化できたので、最適水準の推定を行う。
推定に取り込む要因の指定を行う。既にプーリングを実施し、効果のない要因は排除しているので、残ったすべての項目を選択する。

タブ「推定値」→「推定値プロット」をクリックで以下のようなデータプロットを確認できる。これは一例で、分散分析表の結果に従って表示される要因の組み合わせは変わる。
今回の例では、交互作用はAxBだけが有意であり、交互作用に含まれない主効果は因子C、G、Hが有意であったので、それらのプロットがスタットワークス側で自動で必要と判断され表示されている。

つまり、因子C、G、Hは交互作用を含まないので、単独での水準比較で最適水準が分かる。一方、因子AとBについては交互作用AxBがあるために因子A、Bを単独で評価することには意味がなく、必ず組み合わせた状態で水準効果を比較する必要があるということだ。
推定値プロットの4つのグラフから、今回の最適水準はであることがわかる。
タブ「推定値」→「推定値」で各水準組み合わせによる母平均の点推定値、母平均の95%信頼区間、個々のデータの95%予測区間を確認できる。

残差についても確認し、外れ値がなかったかを検討する
スタットワークスでは分散分析表と推定値以外に「残差」についても確認することができるる。
残差とは、実測値から推定値を引いた値である。(言い換えると「個々の実験生データ」から「その水準での母平均の点推定値」を引いた値)
基準化残差は以下の式で計算できる。
Se:誤差eの平方和 / N:全データ数
基準化残差は、誤差の平均値である0からの離れ具合を見る指標である。
一般にこれが2.5を超える場合は、外れ値と見なし実験条件に誤りがなかったか等を確認する。

実際の例題の残差一覧表を確認する。まず「実測値」は実験データのことであり、「推定値」は対象の水準組み合わせでの母平均の点推定値である。
残差は実測値-推定値で計算される。
そして基準化残差は、上記の計算式で
なので、「残差」を0.205で割った値が「基準化残差」となる。
※0.672は分散分析表の誤差eの平方和(Se)より
「残差」→「正規確率プロット」では、基準化残差の正規性を表示できる。
正規確率座標上にデータが右上がり45°で直線的にプロットされる時、データは正規分布であるとみなされる。
右側には基本統計量と正規性検定による検定統計量とP値が表示される。P値の値から解析対象の特性値が正規分布に従っているかを判断する。

