実験計画法におけるプーリングとは
プーリングとは、効果のない項を誤差と見なして、それらの平方和と自由度を誤差項の平方和と自由度に足し込み、新たな誤差分散を求める作業である。
これにより、誤差の自由度が増え、誤差分散の推定精度が上がる。
このように、効果のないと判断された要因を誤差に足し合わせて誤差を再評価することをプーリングといいます。
プーリングの仕方(計算方法)を分析分析表を用いて確認
では、実際にプーリング作業を行ってみる。
今回はStatWroks(スタットワークス)の要因配置実験を例とするが、エクセルでの計算や直交配列表実験でも基本の考え方は同じである。
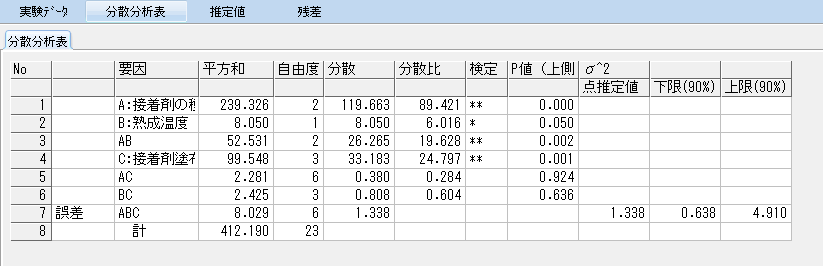
三元配置実験の分散分析表として以下のようなものがあるとする。
(スタットワークスでは、検定列に「*」とあるものが5%で有意、「**」とあるものが1%で有意であることを示す)
これらの内、要因A、B、Cの主効果と交互作用AxBについては影響があることがわかるが、AxC、BxCについては効果が小さい。
交互作用AxC、BxCについては要因効果がないと判断したので、その要因のばらつきは誤差のばらつきの一部と見なし、プーリングの対象とする。
プーリングの考え方は、効果のない項を誤差と見なして、それらの平方和と自由度を誤差項の平方和と自由度に足し込み、新たな誤差分散を求めることである。
具体例として先ほどの分散分析表でどの部分が該当するかを以下に示した。
つまり、プーリング対象のAxC、BxCの平方和と自由度(赤色の枠)を7行目の誤差項の平方和と自由度(青色の枠)に加算する。

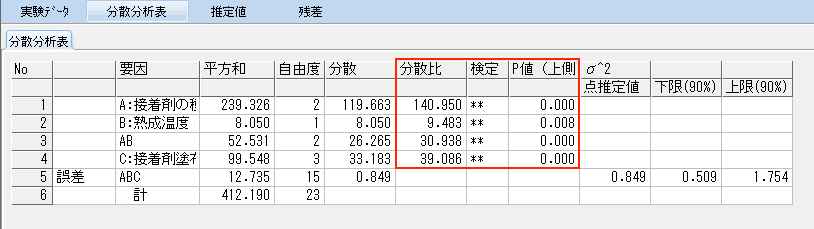
プーリングによる再計算で、
誤差項の平方和は 8.029+2.281+2.425=12.735
自由度は 6+6+3=15 となる。
プーリングの分散分析表を以下に示す。
5行目:誤差項の平方和と自由度がプーリング前より大きくなったことで、赤色の枠で示した各要因の分散比とP値が変わっているのがわかる。
分散比が変わったことで、検定結果(F分布による検定)も再評価されている。
これが実験計画法におけるプーリングの実施方法である。
二元配置実験においては、誤差の自由度が10程度確保されていることが多いので、交互作用はプールしないのが一般的である。
多元配置実験または直交配列表実験においては、効果の小さい要因は上記の基準で積極的にプーリングを行った方が良い。その際、交互作用が有意となった場合には、関連する主効果はプールしない。
直交配列表実験では、一般に誤差の自由度は小さく、第1種の過誤が大きくなる傾向にあるので、有意でない要因は積極的にプールした方が良い。
プーリングをするかどうかには基準がある
プーリングは効果がないと判断できた要因のみを対象にする。
有意とならなかった要因をプーリングの対象とするわけではない。有意とならなかったからといって、効果が”ない”というわけではないためだ。
プーリングをするかどうかの絶対的な基準は存在しないが、慣例的に用いられているルールには以下のものがある。
1.分散比(=値)が2.0以下
2.P値が20%以上
基本は上記の考えに沿って処理がされることが多い。ちなみにスタットワークスの「自動プーリング」機能でもデフォルトでは上記が基準として用いられている。

ただし、以下のようなパターンでは少し考え方が異なる場合がある。
◆交互作用があるときは対応する主効果はプーリングしない
交互作用AxCと因子Aの主効果が有意であった場合、仮に因子Cの主効果は有意でなかったとしてもプーリングしてはいけない。
交互作用があるときには、最適な水準組み合わせを決める際にそれぞれの因子の水準を設定することにななるため、対応する主効果はプーリングの対象とせずそのまま残す必要がある。
◆主効果のプーリングは実験の種類によって考え方が異なる
主効果に対するプーリングの考え方は、二元配置実験のような要因配置実験と、直交配列表実験のような部分配置実験では異なる。
要因配置実験では、取り上げた因子のすべての組み合わせで実験をする。実験回数も多くなることから、データに影響を与えていると思われる因子だけを取り上げて実験するのが一般的である。
一方、部分配置型の直交配列表実験では、どの因子が影響を与えているかを調べる実験であり、効果があるかどうか分からない要因も取り上げて実験する。そのため効果がないと判断されれば、主効果でも交互作用でも積極的にプーリングするという実験そのものの特性による違いがある。

![図解入門 よくわかる最新実験計画法の基本と仕組み[第2版] 図解入門 よくわかる最新実験計画法の基本と仕組み[第2版]](https://m.media-amazon.com/images/I/514nRQSv1sL._SL160_.jpg)