母集団の分散の状態(既知or未知)によって検定手法が異なる
正規分布する母集団からランダムサンプリングされたn個の標本(データ)があるとき、標本平均が、母集団の母平均
との差の有無を検定する場合の検定統計量は以下の通り。
◆母集団の分散が既知の場合:Z検定統計量(標準正規分布)
◆母集団の分散が未知の場合:t検定統計量(t分布)
:母分散 / V:不偏分散
以下、母集団の平均値に関する検定について3つの具体例で確認する。
◆【例1】母集団の分散が既知:平均値が変わったかどうかについての検定
母平均=13.2、母分散=1の母集団からn=9の標本をランダムサンプリングにより取得した結果、標本平均
=13.9であった。ばらつきは変化していないとする。このとき、平均値が変化したかどうかを検定する。
□仮説の設定
帰無仮説 :
(
=13.2)
対立仮説 :
□有意水準の設定
α:第1種の誤りを5%とする
□棄却域の確認
→ 両側検定
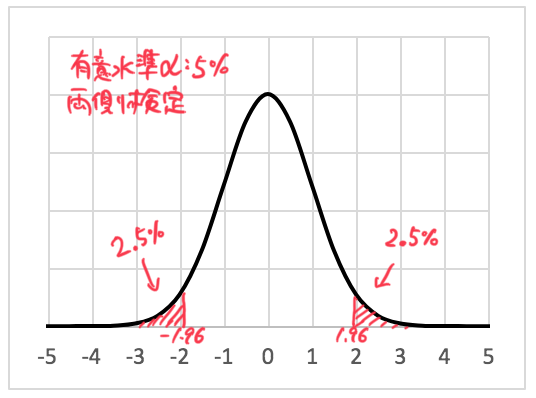
両側検定で5%なので、上図のように正規分布の両側2.5%ずつの領域が棄却域となる。
棄却限界値は1.960となる。正規分布表が手元にあればそちらを参照するか、なくてもエクセルがあれば関数で計算できる。
NORM.S.INV(確率) → NORM.S.INV(0.025)=-1.960 あるいは、NORM.S.INV(0.975)=1.960で求めることができる。
□検定統計量の計算(例題は分散が既知なのでZ検定統計量)と”判定”
標準正規分布の棄却域とZ検定統計量を比較すると、
2.10 > 1.96なので有意水準5%でこの検定は有意であり帰無仮説は棄却され、対立仮説
が採択される。
よって、平均値は変わったと判定する。
◆【例2】母集団の分散が既知:平均値が大きくなったかどうかについての検定
母平均=13.2、母分散=1の母集団からn=9の標本をランダムサンプリングにより取得した結果、標本平均
=13.9であった。ばらつきは変化していないとする。このとき、平均値が大きくなったかどうかを検定する。
□仮説の設定
帰無仮説 :
(
=13.2)
対立仮説 :
>
□有意水準の設定
α:第1種の誤りを5%とする
□棄却域の確認
>
→ 右片側検定
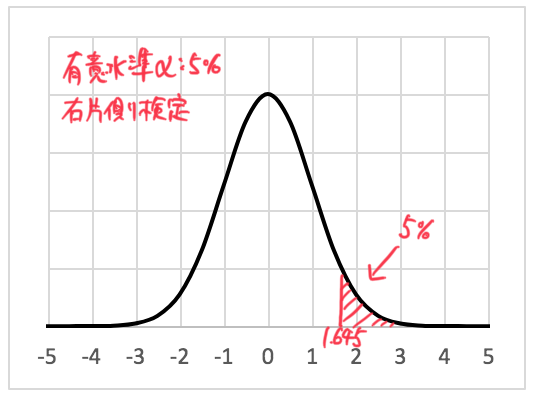
右片側検定で有意水準5%なので、上図のように正規分布の右側5%より外の領域が棄却域となる。
棄却限界値は1.645となる。正規分布表が手元にあればそちらを参照するか、なくてもエクセルがあればNORM.S.INV(確率) → NORM.S.INV(0.95)=1.645で求めることができる。
*ちなみに、NORM.S.INVは標準正規分布に関する関数で、標準正規分布とは平均0、分散である。
よって、NORM.INV(確率,平均,標準偏差)=NORM.INV(0.95,0,1)としても、1.645と同じ結果を得ることができる。
□検定統計量の計算(例題は分散が既知なのでZ検定統計量)と”判定”
標準正規分布の棄却域とZ検定統計量を比較すると、
2.10 > 1.645なので有意水準5%でこの検定は有意であり帰無仮説は棄却され、対立仮説
>
が採択される。
よって、平均値は大きくなったと判定する。
◆【例3】母集団の分散が未知:平均値が大きくなったかどうかについての検定
母平均=13.2の母集団からn=9の標本をランダムサンプリングにより取得した結果、標本平均
=13.9、不偏分散V=4.0であった。このとき、平均値が大きくなったかどうかを検定する。
□仮説の設定
帰無仮説 :
(
=13.2)
対立仮説 :
>
□有意水準の設定
α:第1種の誤りを5%とする
□棄却域の確認
>
→ 右片側検定
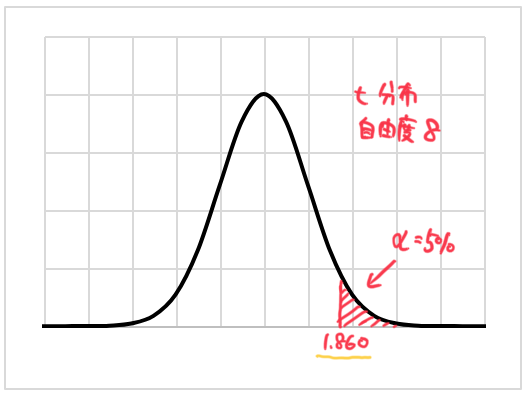
右片側検定で有意水準5%なので、上図のようにt分布の右側5%より外の領域が棄却域となる。(母集団の分散が”未知”なのでt検定)
自由度はサンプルサイズ-1=9-1=8である。
棄却限界値はt分布表から確認するか、エクセル関数で以下のように求める。
T.INV(確率,自由度)=T.INV(0.95,8)=1.86
よって、棄却限界値は1.86となる。
*T.INVは左片側確率%点を求める関数なので「-T.INV(0.05,8)」としても良い。
□検定統計量の計算(例題は分散が未知なのでt検定統計量)と”判定”
t分布の棄却域とt検定統計量を比較すると、
1.05 < 1.86なので有意水準5%でこの検定は有意とはいえず、帰無仮説は棄却されない。
よって、平均値は大きくなったとは判定できない。
