◆繰返し数が等しい場合の一元配置実験(p12)
[例1.2:化学薬品の収率]
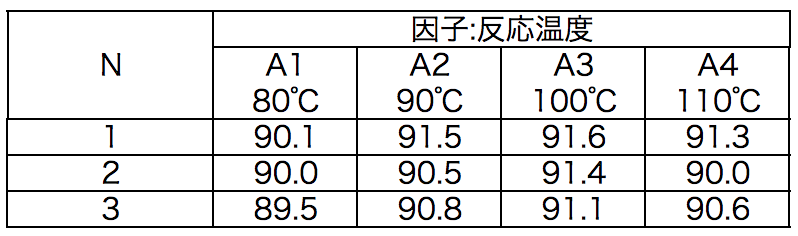
ある化学薬品の合成工程がある。いま反応温度(A1:80℃、A2:90℃、A3:100℃、A4:110℃)を因子に取り上げ、収率を高めるための実験を行った。実験は各温度で3回ずつ繰り返して行われ、また、計12回の実験はランダムな順序で行われた。収率に対する反応温度の効果を解析せよ。
得られたデータ
この例題をStatWorks(スタットワークス)を使って解析する。
ちなみにエクセルのみで解析する場合は、下記の記事の通り。
エクセルだと、データプロット(散布図)を作成したり、信頼区間や予測区間の数式を理解して煩雑な計算をしないといけないが、スタットワークスだと実験データの入力の手間だけで、解析自体は一瞬のうちに完了する。
当然だが、どちらのパターンでも最終的に得られる結果はまったく同じである。
スタットワークスを用いた一元配置実験 解析手順
ソフトを起動して、新規のワークシートを開く。
実験で得られたデータを入力。今回はスタットワークス上でテキストの数字を手入力したが、別でCSVファイルなどある場合はインポートすれば良い。
入力した結果を以下に示す。
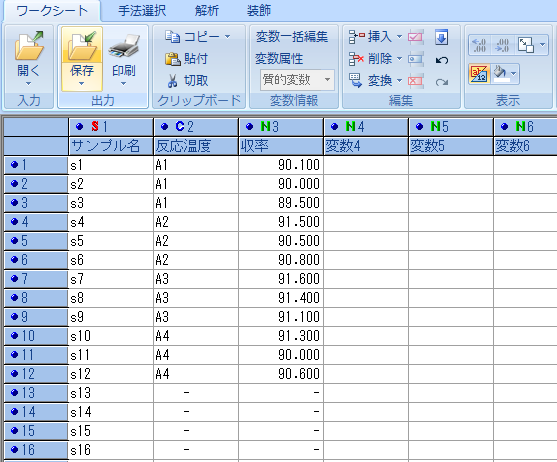
2列目は実験条件(今回の例題では因子A:合成工程の反応温度)なので、質的変数にしている。変数を帰るのは「変数属性」をクリックすれば良い。
3列目の収率は量的変数のままとしている。
ストットワークスでは、質的変数は「C」、量的変数は「N」と表現される。
データの入力が済んだので解析に入る。
上タブの「手法選択」→「実験計画法」→「一元配置分散分析」を選択する。
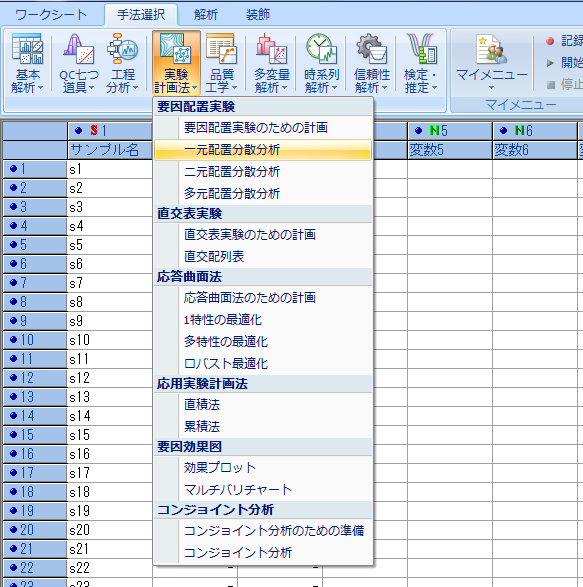
「変数の指定」ウィンドウが表示されるので項目をクリックして左から右に仕分けをする。
今回の例題では特性値に「収率」 実験条件に「反応温度」をそれぞれ移動させた。Noというのはワークシートの列数に対応している。
移動ができたら「次へ進む」をクリック。解析が実行される。
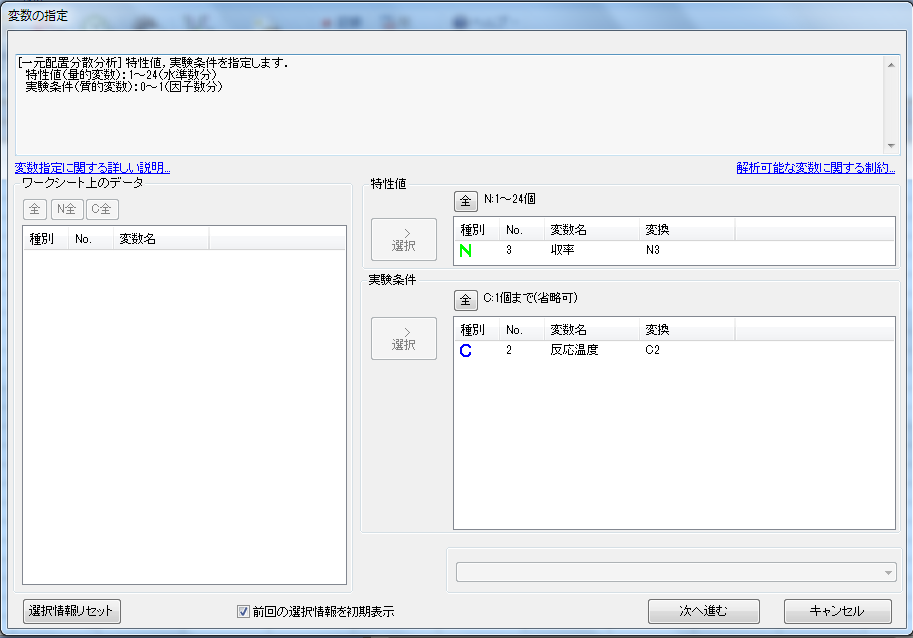
今回の解析対象の実験データ一覧が表示される。
因子A:反応温度で、実験繰り返し数はどの水準とも各3回だ。
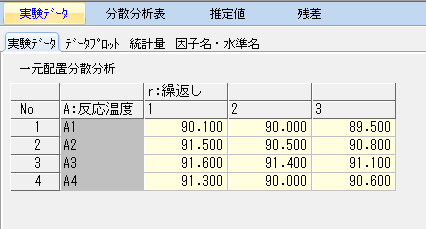
「実験データ」→「データプロット」で散布図グラフを確認できる。
横軸は因子Aの各水準、縦軸は収率(%)となる。合成工程の収率なので、値は高い方が特性として良い。
グラフで「×」は生データプロット、「○」は各水準平均を示している。さらに、線は水準間の平均値結線、赤色の横線は全体データの平均を示している。
グラフから、反応温度による収率の効果(=因子Aの主効果)はありそうだとわかる。
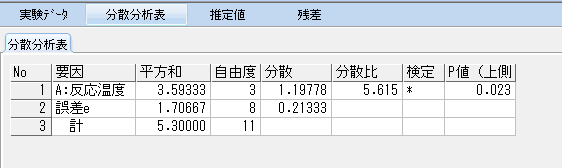
タブの「分散分析表」をクリックして、分散分析結果の確認をする。エクセルでの解析に比べ、スタットワークスは検定結果とP値まで瞬時に導き出せるのが便利だ。
検定結果に「*」とあるので、因子Aは5%で有意であることがわかる。
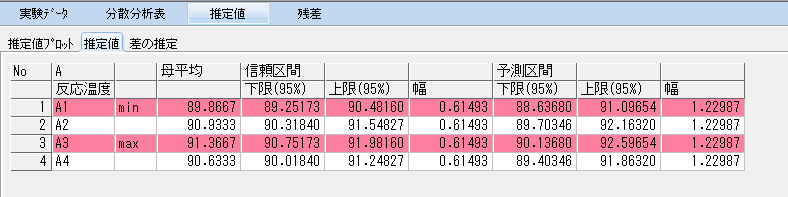
次にタブの「推定値」→「推定値」をクリックして、因子Aの各水準の推定値を確認する。表の「母平均」は実験データ(今回の例題では繰り返し3回)の平均値を意味する。
各水準の母平均の95%信頼区間、個々のデータについての95%予測区間が確認できる。
実務に活かす目的なら解析”結果”だけでも構わないが、信頼区間と予測区間がそれぞれどのような計算方法なのか知りたい場合は、同じ例題をエクセルで解析した以下の記事を参照されたい。
タブ「推定値」→「推定値プロット」で横軸:因子A各水準、縦軸:収率が確認できる。「○」のプロットは母平均の点推定値で、上下の矢印が区間を示している。今回の例題では繰り返しが3回であったが、繰り返し数が多いほどより幅の狭い推定ができる。
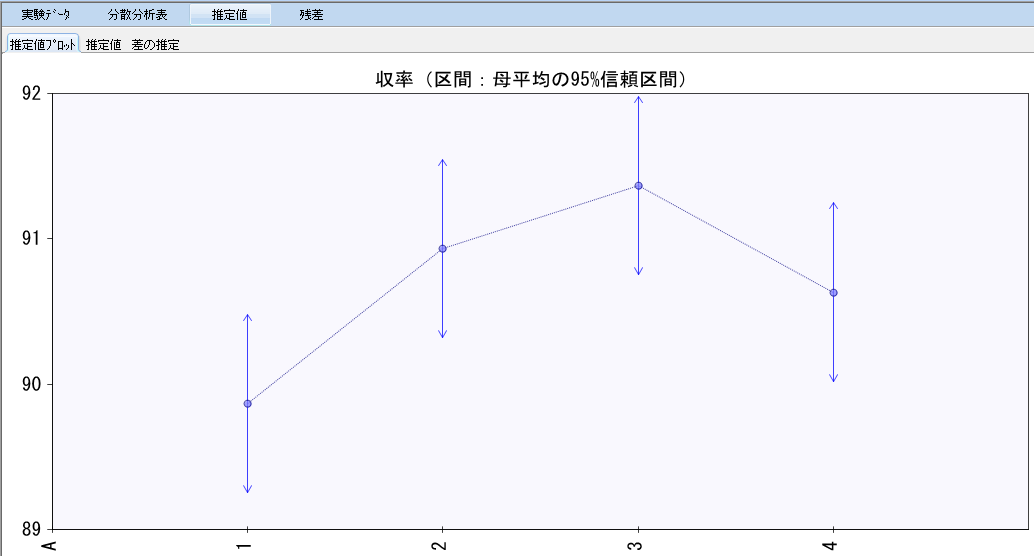
よって、化学薬品の合成工程で反応温度による収率の差はあり、最適水準はA3(100℃)でその時の母平均の点推定値は91.37%である。
残差とは
スタットワークスでは分散分析と推定値以外に「残差」についても確認することができるる。
残差とは、実測値から推定値を引いた値である。(言い換えると「個々の実験生データ」から「その水準での母平均の点推定値」を引いた値)
また残差t値は以下の式で計算できる。
Se:誤差eの平方和 / N:全データ数
t値は誤差の平均値である0からの離れ具合を見る指標である。
慣例的にこれが2.5を超える場合は、外れ値と見なし実験条件に誤りがなかったか等を確認する。
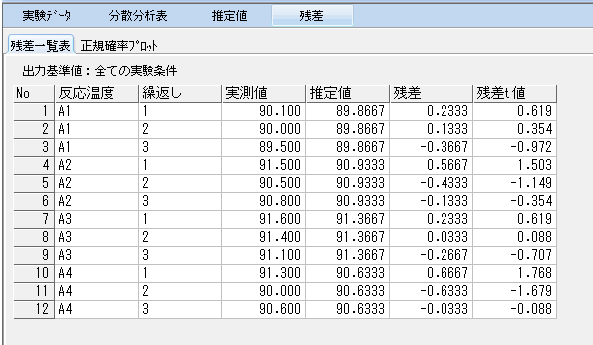
実際の例題の残差一覧表を確認する。
まず「実測値」は実験データのことであり、「推定値」は因子A各水準での母平均の点推定値である。この場合の点推定値とは、繰り返し3回の実験生データの平均値を意味する。
「残差」は実測値-推定値で計算される。
最後に残差t値は、上記の計算式だが
なので、「残差」を0.377で割った値が「残差t値」となる。
※1.70667は分散分析表の誤差eの平方和を参照。
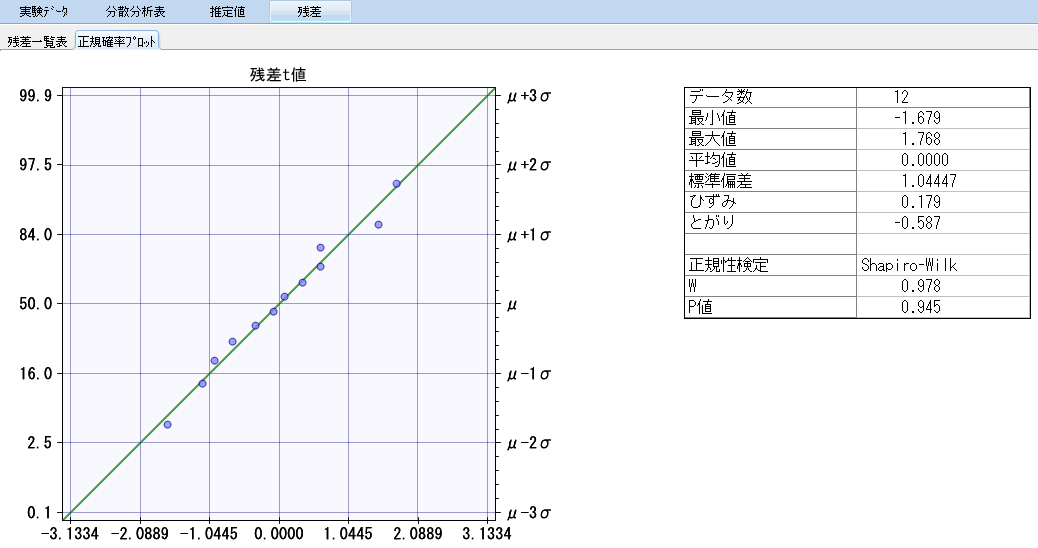
「残差」→「正規確率プロット」で、t値の正規性の確認ができる。
正規確率座標上にデータが右上がり45°で直線的にプロットされる時、データは正規分布であるとみなされる。
右側には基本統計量と正規性検定による検定統計量とP値が表示される。P値の値から解析対象の特性値が正規分布に従っているかを判断する。