[例3.2:合成樹脂の歩留りに関する繰り返しのある三元配置法]-p47
K社では合成樹脂の製造を行なっており、その歩留まりの向上が生産技術部門の重要な課題となっている。そこで、歩留まりに影響のありそうな因子を取り上げ、実験で最適条件を見つけることにした。因子と水準は下記の図の通りである。なお、各水準組み合わせで2回繰り返すことにし、繰り返しのある三元配置実験で行なった。これを解析せよ。
因子と水準

得られた実験データ
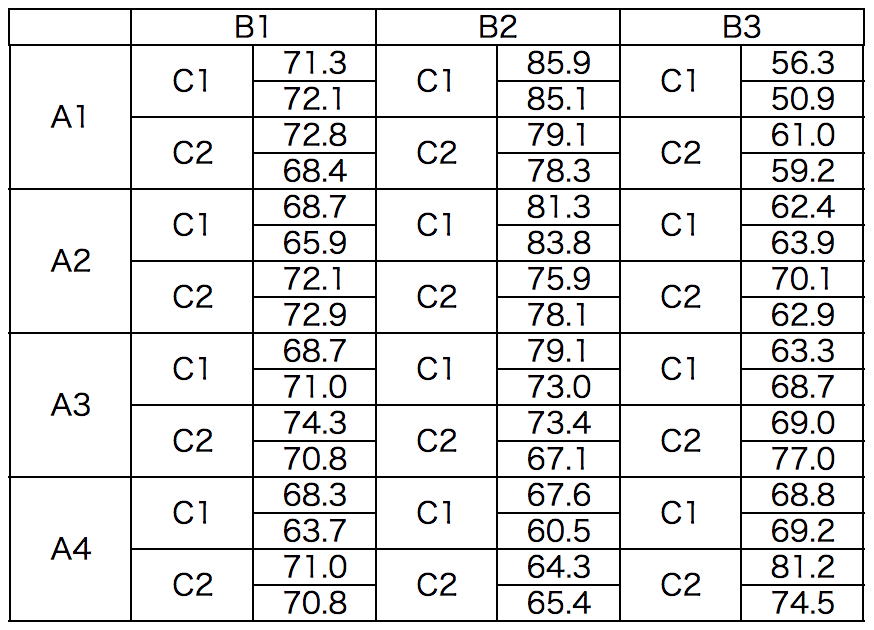
この例題をStatWorks(スタットワークス)を用いて解析していく。
「繰り返しがある」とは?
三元配置実験で繰り返しがある場合とない場合で異なるのは、3因子の交互作用を検出できるかである。
繰り返しがあると、AxBxCという三元配置実験における因子数の最も多い交互作用が検出できるのに対して、繰り返しがないとそれが誤差と交絡し検出できなくなるという部分に違いがある。
一般に3因子以上の交互作用が存在することは少なく、また技術的に解釈することが難しいので多元配置実験においては繰り返しを入れないで実験を行うことの方が多い。
繰り返しのある三元配置実験の分散分析表は以下の表のようになる。

スタットワークス(StatWorks)による多元配置分散分析の解析手順
ソフトを起動して、新規のワークシートを立ち上げる。
まずは解析するワークシートの作成からはじめる。既に実施済みの外部データがCSVなどであればそれをインポートしても良いが、今回はテキストの実験データと同じものをスタットワークス上で作成する。
上タブ「手法選択」→「実験計画法」→「要因配置実験のための計画」を選択。

「因子の設定」ウィンドウが表示される。左上の黄色の四角ボタンをクリックして、任意の因子を作成していく。
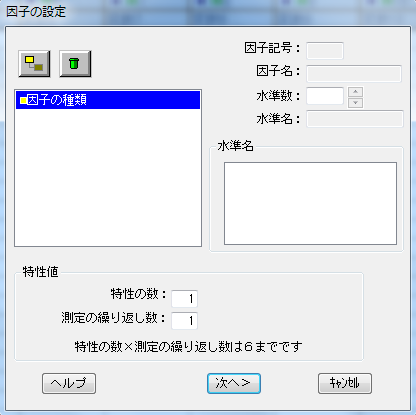
今回の例題に沿って因子の作成が完了。
因子A:重合温度 4水準
因子B:触媒の種類 3水準
因子C:原材料メーカー 2水準 が解析対象である。
ここで一つコツとしては、繰り返しのある要因配置実験の場合、因子A~Cに加えてもう一つ変数を追加し、それを繰り返しの情報(水準数=繰り返し回数)を入れておくとその後のワークシートでの作業がしやすくなる。
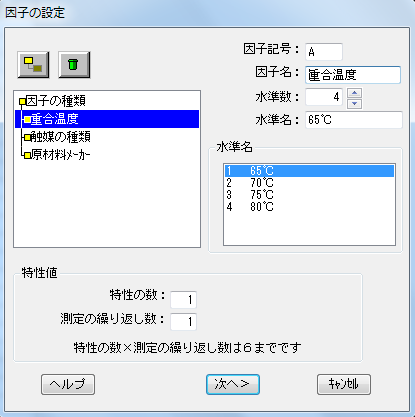
因子の設定が完了したら、リボンにある「4:変数への登録」をクリックで、作成した実験条件の一覧がワークシートへ反映される。

ワークシートに戻る。先ほど作成した因子A~Cの各水準組み合わせの実験条件一覧がワークシートにも展開されていることが確認できる。特性値(歩留まり)に実験データを入力する。
同じ条件の組み合わせが2つずつ並んでいるのは、因子の設定で「繰り返し」の変数を2水準として追加していたためである。下の画像では、6列目に「繰り返し」が表示されていたが、解析には不要なので列削除している。

ここでタブの「番号/名称切換」をクリックするとワークシート上で、各因子の各水準の表示方法を変更することができる。このワークシートを元に実験をする場合は「80℃」のような表記が見やすいし、解析対象としてのみ扱う場合は1から始まる記号としての数字の方が見やすい。表示の仕方だけで中身自体は同じものなので、必要に応じて都度切り替えれば良い。

ワークシートへの実験データ(特性値)の入力が完了したら、解析に移る。
タブ「手法選択」→「実験計画法」→「多元配置分散分析」を選択する。

「変数の指定」ウィンドウが表示される。
デフォルトではワークシートで作成した列データが左側のボックスに一覧として出ている。その中から解析対象の実験条件と特性値を選んで右側に移動させていく。

仕分けが完了したのが以下の状態。
右上の特性値には歩留まり、右下の実験条件には重合温度、触媒の種類、原材料のメーカーの3つを移動させた。ここで「No」とはワークシート上での列番号を意味している。仕分けができたことを完了したら、「次へ進む」をクリックすると解析が実行される。

ここからは解析結果を確認していく。
まずは「実験データ」→「データプロット」で散布図グラフを確認する。今回の例題は三元配置実験を繰り返し2回で実施しているので、AxBxCの3因子交互作用も検出できている。
データプロットだけでも色々なことが推察できる。例えば以下のようなことだ。
・因子B、Cの主効果がありそうである。
・交互作用についてはAxB、BxCがありそうである。
・AxBxC交互作用プロットより最適水準はが有効そうである。(緑色の点)
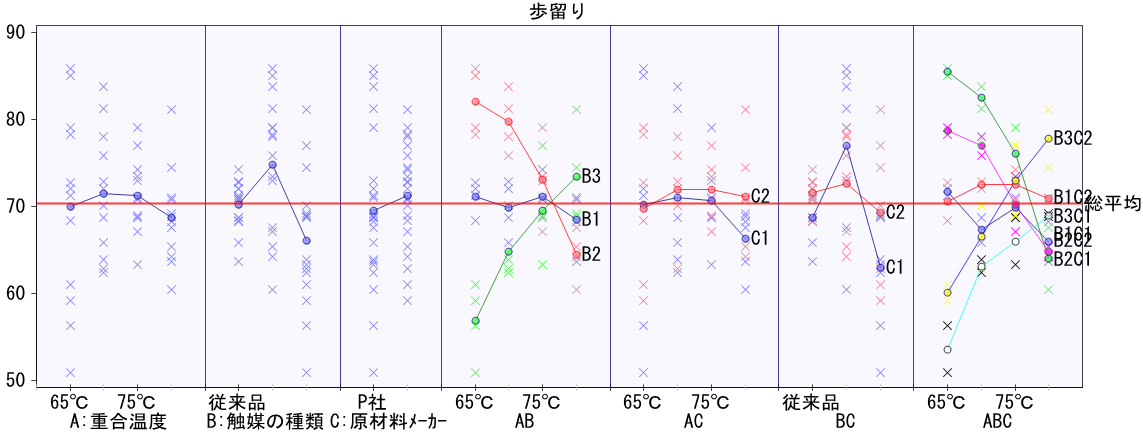
「実験データ」→「統計量」で要因ごとの平均値の計算結果が確認できる。データプロットはこれらを散布図グラフ化したものである。

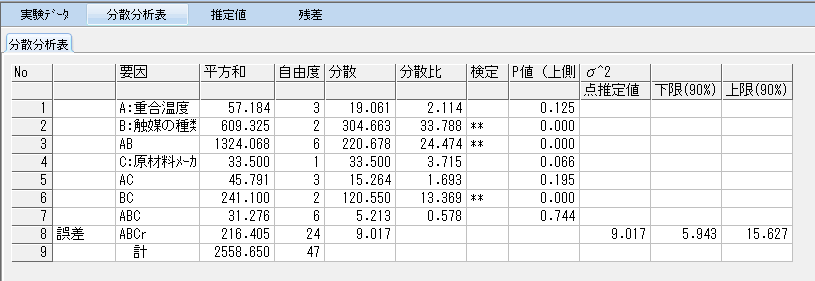
次に分散分析表を確認する。
因子B主効果、交互作用AxB、BxCがF検定の結果1%で有意であることがわかる。
因子AとCについては検定欄に「*」表記がなく5%有意以下であったが、それらの因子を含む交互作用が有意であるためプーリングはせずそのままにしておく。
誤差の自由度は24と比較的大きくこのままでも問題ないのだが、さらに誤差の推定精度を上げるために効果の小さいAxC、AxBxCをプーリングする。
プーリングをしたい要因(=行)を選択して色を変えた状態で、右クリックで表示されるメニューの中からプーリングを選択。

*ここで、プーリングとは、効果のない項を誤差と見なして、それらの平方和と自由度を誤差項の平方和と自由度に足し込み、新たな誤差分散を求める作業である。
これにより、誤差の自由度が増え、誤差分散の推定精度が上がる。
プーリングした結果、再計算された分散分析表が以下である。
B、AxB、BxCが1%有意という検定結果は今回の例題では変わらずであった。

次に推定を行う。プーリング後の分散分析表の誤差項以外のすべての行をクリックして選択状態にして「推定値」をクリック。
各水準組み合わせによる推定値一覧が以下である。母平均の点推定値、母平均の95%信頼区間、個々のデータの95%予測区間、「max」「min」の表記から最適水準とその逆の水準などがわかる。
今回の例では、「65℃、改良品1、P社 」=「」の組み合わせが最適水準であり、データプロットからの予測と一致している。

「推定値プロット」にすると、横軸に因子A~Cの水準組み合わせ、縦軸に特性値を取った母平均の95%信頼区間のグラフ一覧が表示される。

さらに推定値プロットのところで、表示変更を押すと以下のようにグラフが変更される。今回の例ではこう交互作用AxB、BxCが1%で有意であるのでそれらの交互作用の母平均の点推定を結線したものが自動で表示される。
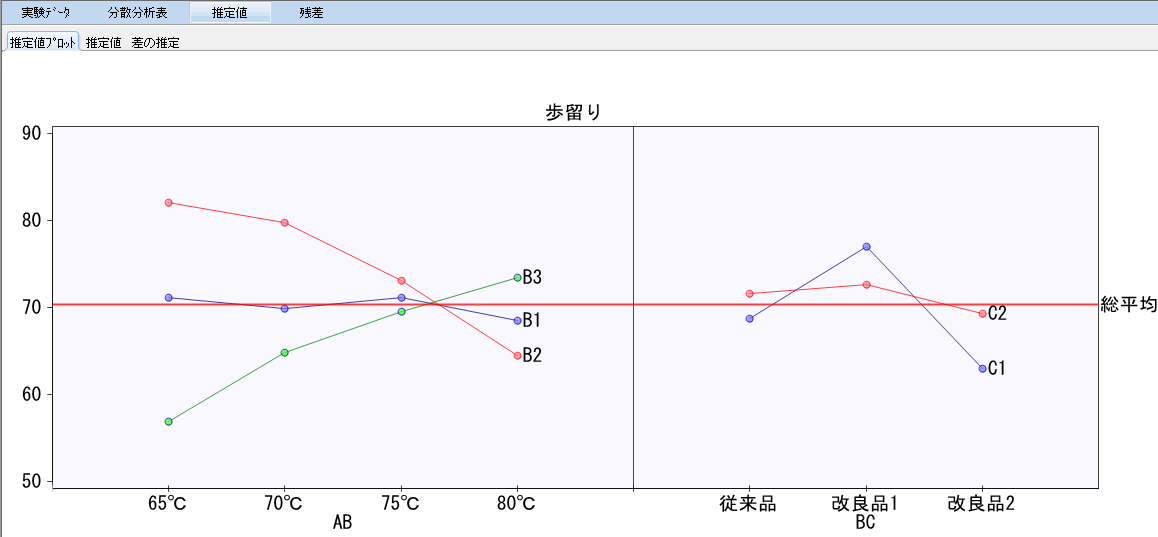
最後にタブの「残差」→「残差一覧表」で、各水準組み合わせの残差とt値について確認する。
残差とは、実測値から推定値を引いた値である。(言い換えると「個々の実験生データ」から「その水準での母平均の点推定値」を引いた値)
また残差t値は以下の式で計算できる。
Se:誤差eの平方和 / N:全データ数
t値は誤差の平均値である0からの離れ具合を見る指標である。
慣例的にこれが2.5を超える場合は、外れ値と見なし実験条件に誤りがなかったか等を確認する。
実際の例題の残差一覧表を確認する。まず「実測値」は実験データのことであり、「推定値」は因子A各水準での母平均の点推定値である。
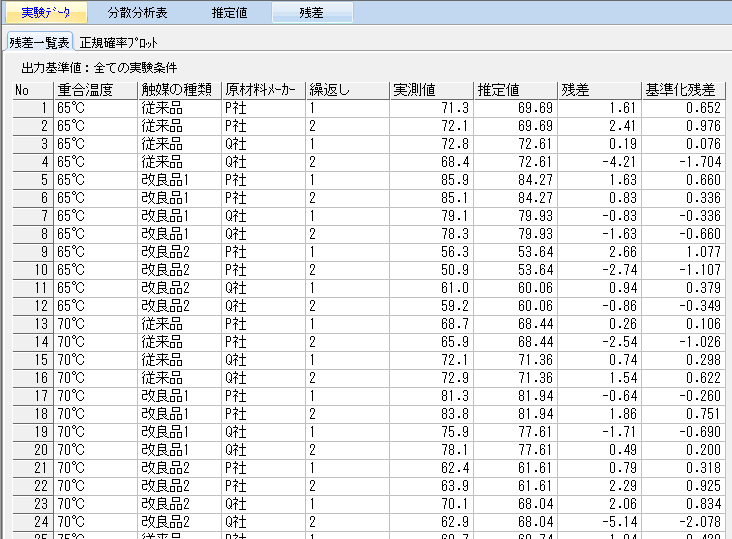
「残差」→「正規確率プロット」では、t値の正規性を表示できる。
正規確率座標上にデータが右上がり45°で直線的にプロットされる時、データは正規分布であるとみなされる。右側には基本統計量と正規性検定による検定統計量とP値が表示される。P値の値から解析対象の特性値が正規分布に従っているかを判断する。

